Question 9:
(a) Diagram 6 shows the rectangle ABCD.
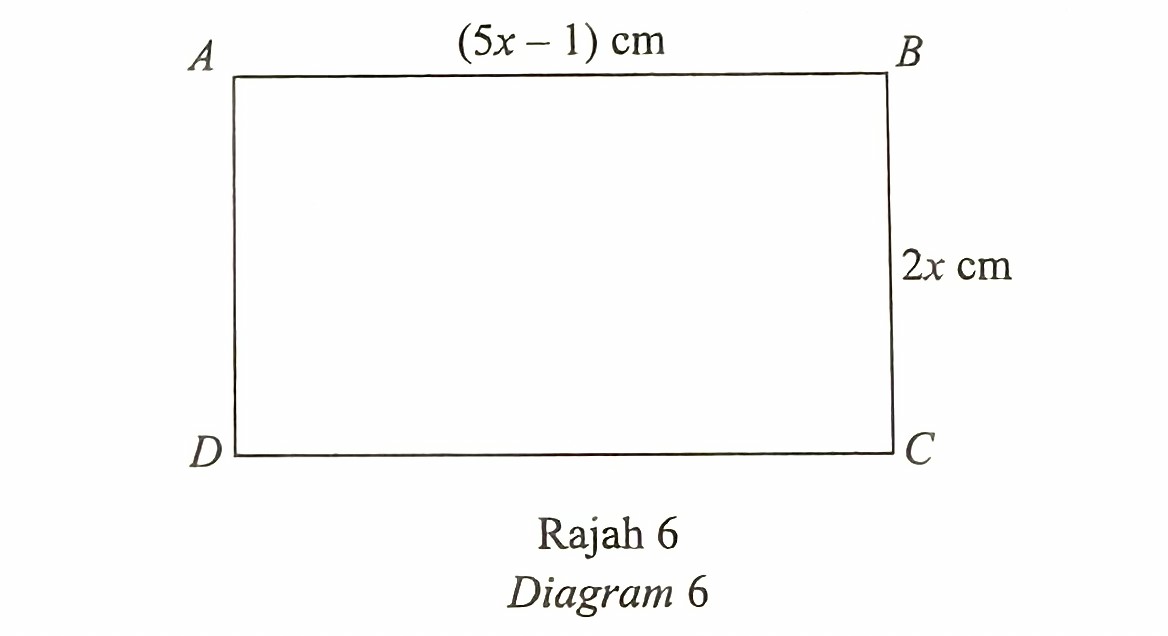
At an instant, the value of x changes from 3 cm to (3 + p) cm, such that p is a small value.
Using differentiation, express in terms of p, the small change in the area of ABCD, in cm2, at that instant.
[3 marks]
(b) Diagram 7 shows two lots of land, P and Q. Both lots will be planted completely with the same type of grass.
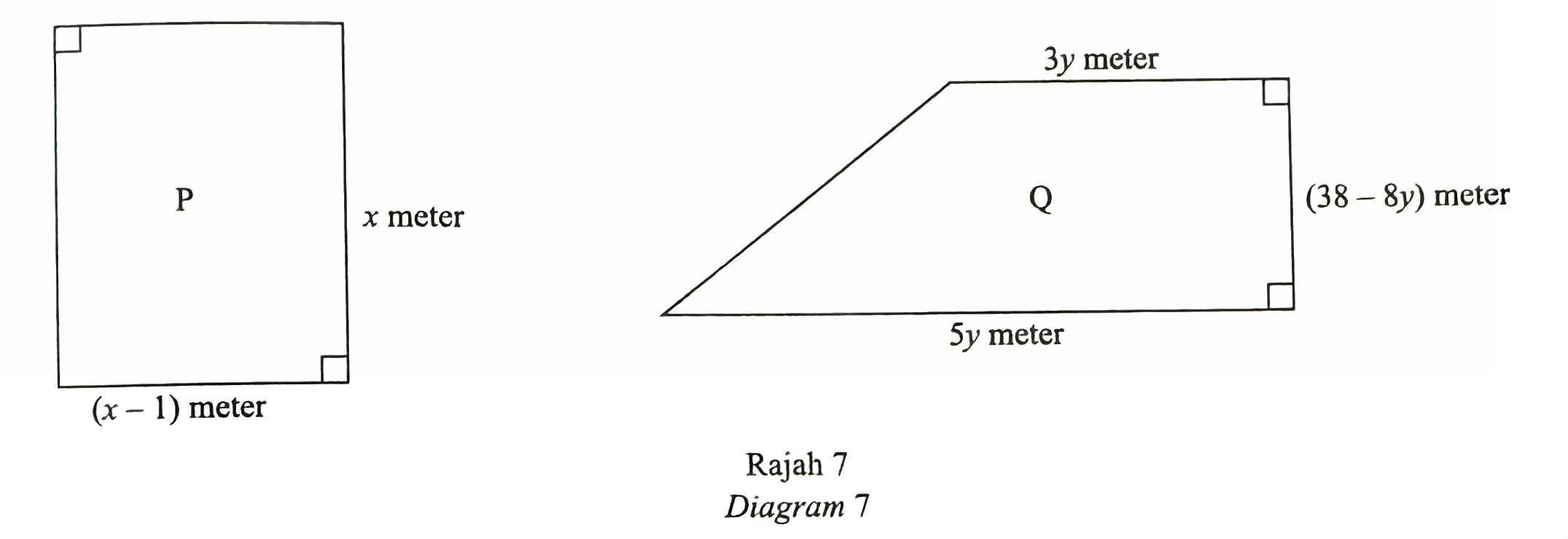
It is given that the perimeter of lot P is 54 m and the area of lot Q is A m2.
(i) Using differentiation, find the value of y, such that A is a maximum.
(ii) Hence, determine the lot that will be planted with the most grass. Justify your answer.
[6 marks]
Answer:
(a)
$$ \begin{aligned} & Area, A=2 x(5 x-1) \\ & A=10 x^2-2 x \end{aligned} $$
$$ \begin{aligned} & \frac{\mathrm{d} A}{\mathrm{~d} x}=20 x-2 \\ & \text { When } x=3, \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=20(3)-2 \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=58 \end{aligned} $$
$$ \begin{aligned} & \frac{\delta A}{\delta x} \approx \frac{\mathrm{~d} A}{\mathrm{~d} x} \\ & \delta A=\frac{\mathrm{d} A}{\mathrm{~d} x} \times \delta x \\ & \delta A=(58)[(3+p)-3] \\ & \delta A=(58)(p) \\ & \delta A=58 p \end{aligned} $$
(b)(i)
$$ \begin{aligned} A & =\frac{1}{2}(3 y+5 y)(38-8 y) \\ & =\frac{1}{2}(8 y)(38-8 y) \\ & =4 y(38-8 y) \\ & =152 y-32 y^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} A}{\mathrm{~d} y}: 152-64 y & =0 \\ -64 y & =-152 \\ y & =\frac{-152}{-64} \\ y & =2.375 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\frac{\mathrm{d}^2 A}{\mathrm{~d} y^2}=-64<0\\ &\therefore A \text { is maximum when } y=2.375 \mathrm{~m} \text {. } \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \text { Area of } Q & =152 y-32 y^2 \\ & =152(2.375)-32(2.375)^2 \\ & =180.5 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter, } P=54 \mathrm{~m}\\ &\begin{aligned} 2[(x-1)+x] & =54 \\ 2(2 x-1) & =54 \\ 2 x-1 & =27 \\ 2 x & =28 \\ x & =14 \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Area of } P & =(x-1)(x) \\ & =(14-1)(14) \\ & =182 \mathrm{~m}^2 \end{aligned} $$
Lot P will be planted with most grass because the area of P is 182 m2, which 1.5 m2 more than the area of Q, which is 180.5 m2.
(a) Diagram 6 shows the rectangle ABCD.

At an instant, the value of x changes from 3 cm to (3 + p) cm, such that p is a small value.
Using differentiation, express in terms of p, the small change in the area of ABCD, in cm2, at that instant.
[3 marks]
(b) Diagram 7 shows two lots of land, P and Q. Both lots will be planted completely with the same type of grass.

It is given that the perimeter of lot P is 54 m and the area of lot Q is A m2.
(i) Using differentiation, find the value of y, such that A is a maximum.
(ii) Hence, determine the lot that will be planted with the most grass. Justify your answer.
[6 marks]
Answer:
(a)
$$ \begin{aligned} & Area, A=2 x(5 x-1) \\ & A=10 x^2-2 x \end{aligned} $$
$$ \begin{aligned} & \frac{\mathrm{d} A}{\mathrm{~d} x}=20 x-2 \\ & \text { When } x=3, \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=20(3)-2 \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=58 \end{aligned} $$
$$ \begin{aligned} & \frac{\delta A}{\delta x} \approx \frac{\mathrm{~d} A}{\mathrm{~d} x} \\ & \delta A=\frac{\mathrm{d} A}{\mathrm{~d} x} \times \delta x \\ & \delta A=(58)[(3+p)-3] \\ & \delta A=(58)(p) \\ & \delta A=58 p \end{aligned} $$
(b)(i)
$$ \begin{aligned} A & =\frac{1}{2}(3 y+5 y)(38-8 y) \\ & =\frac{1}{2}(8 y)(38-8 y) \\ & =4 y(38-8 y) \\ & =152 y-32 y^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} A}{\mathrm{~d} y}: 152-64 y & =0 \\ -64 y & =-152 \\ y & =\frac{-152}{-64} \\ y & =2.375 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\frac{\mathrm{d}^2 A}{\mathrm{~d} y^2}=-64<0\\ &\therefore A \text { is maximum when } y=2.375 \mathrm{~m} \text {. } \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \text { Area of } Q & =152 y-32 y^2 \\ & =152(2.375)-32(2.375)^2 \\ & =180.5 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter, } P=54 \mathrm{~m}\\ &\begin{aligned} 2[(x-1)+x] & =54 \\ 2(2 x-1) & =54 \\ 2 x-1 & =27 \\ 2 x & =28 \\ x & =14 \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Area of } P & =(x-1)(x) \\ & =(14-1)(14) \\ & =182 \mathrm{~m}^2 \end{aligned} $$
Lot P will be planted with most grass because the area of P is 182 m2, which 1.5 m2 more than the area of Q, which is 180.5 m2.