Question 3:
(a)
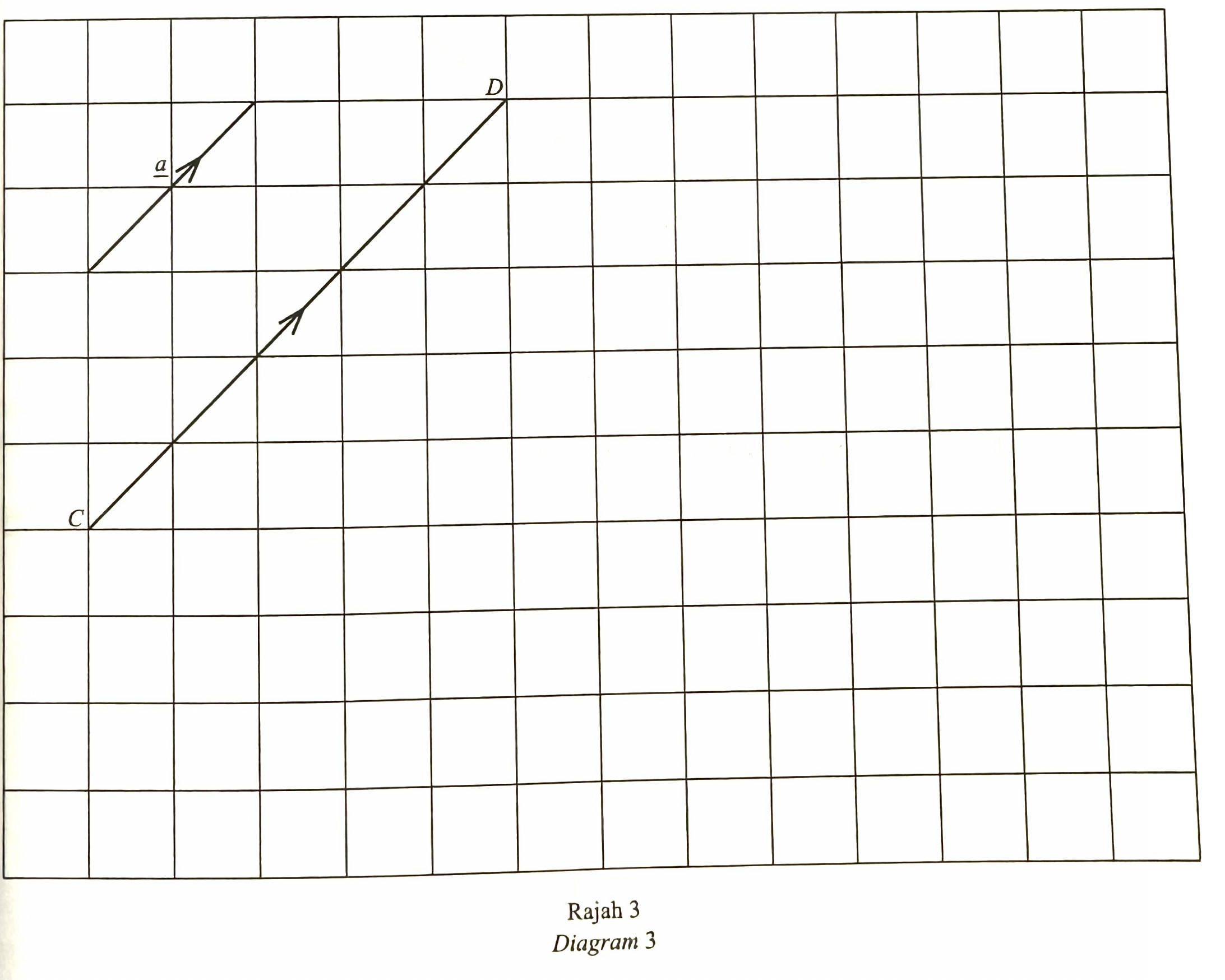
$$ \text { Diagram } 3 \text { shows } \underline{a} \text { and } \stackrel{\rightharpoonup}{C D} \text { on a square grid. } $$
(i)
$$ \text { Express } \stackrel{\rightharpoonup}{C D} \text { in terms of } \underline{a} \text {. } $$
(ii)
$$ \text { Draw }-4 \underline{a} \text { on Diagram } 3 . $$
[2 marks]
(b) Solutions by scale drawing and / or vector are not accepted.
Diagram 4 shows the straight line AB.
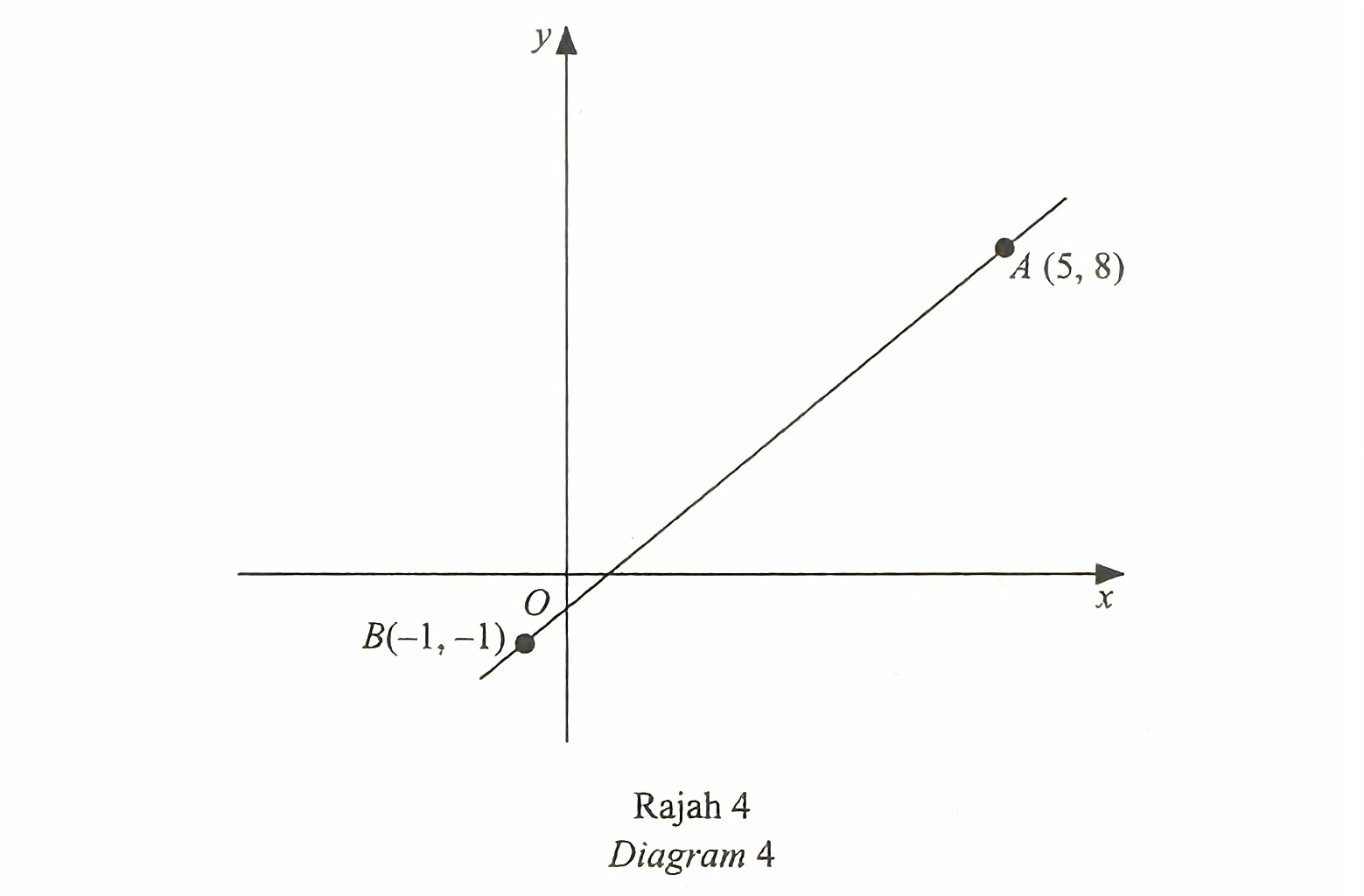Given that point C lies on AB such that AC : CB = 2 : 1, find the coordinates of C.
[2 marks]
(c) Solutions by scale drawing is not accepted.
It is given that P(4, 5) and Q(2, 1) line on a Cartesian plane.
Find the equation of the straight line which is perpendicular to the straight line PQ and passing through point P.
[3 marks]
Answer:
(a)(i)
$$ \begin{aligned} & \overrightarrow{C D}=\underline{a}+\underline{a}+\frac{1}{2} \underline{a} \\ & \overrightarrow{C D}=\frac{5}{2} \underline{a} \end{aligned} $$
(a)(ii)
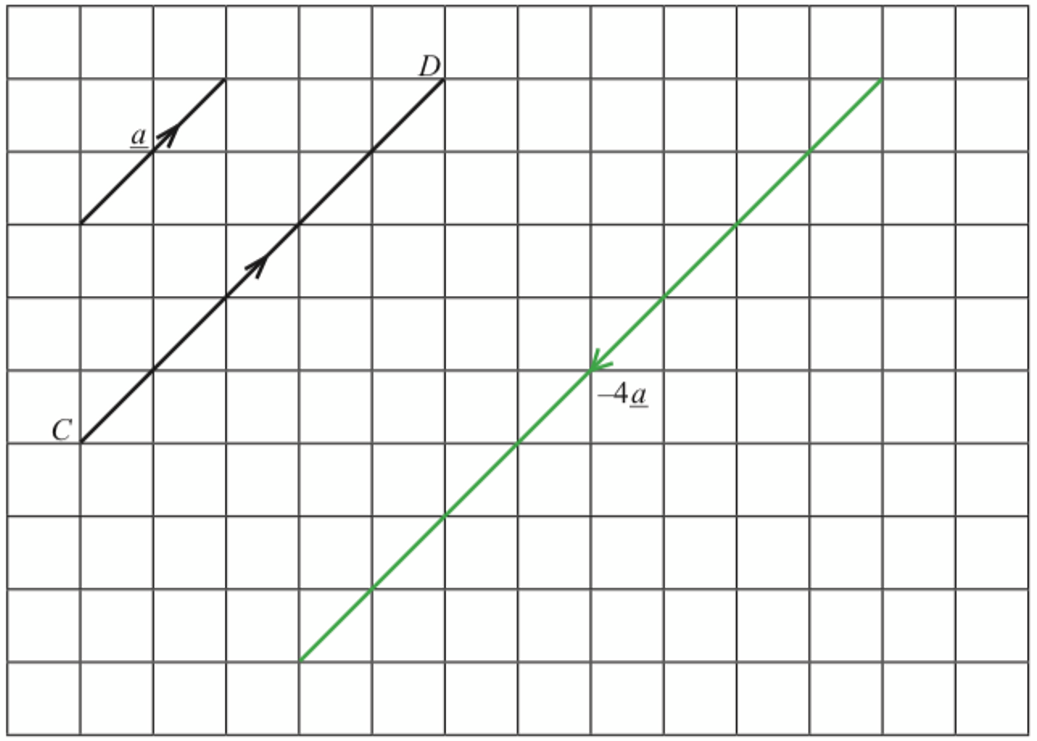
(b)
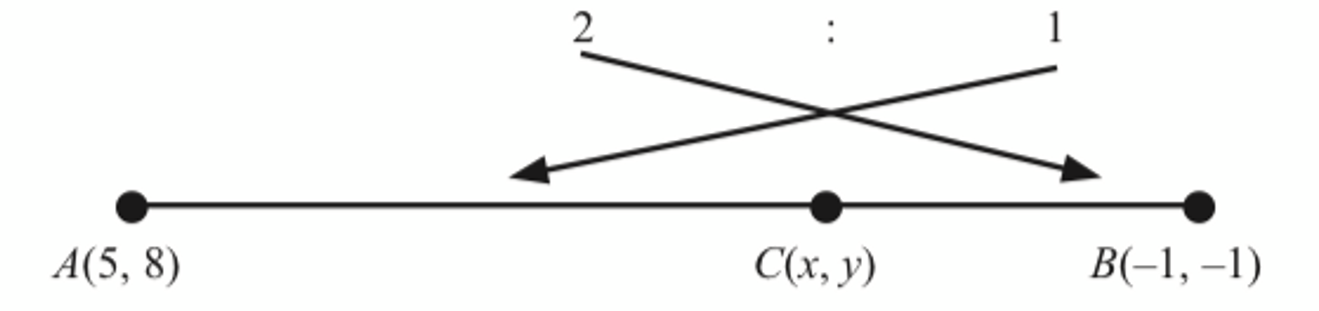
$$ \begin{aligned} C(x, y) & =\left(\frac{2(-1)+(1)(5)}{2+1}, \frac{(2)(-1)+(1)(8)}{2+1}\right) \\ & =(1,2) \end{aligned} $$
(c)
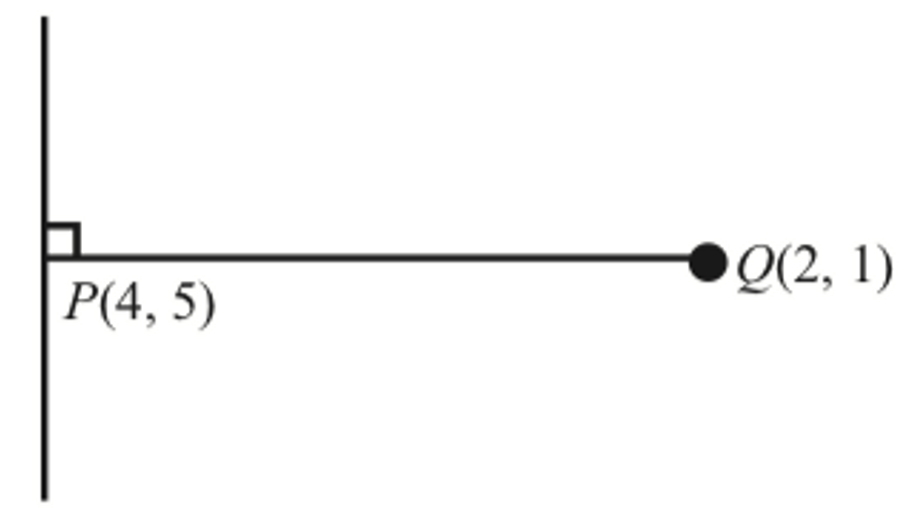
$$ \begin{aligned} m_{P Q} & =\frac{5-1}{4-2} \\ & =2 \end{aligned} $$
$$ \begin{aligned} m_{P Q} \times m_2 & =-1 \\ 2 \times m_2 & =-1 \\ m_2 & =-\frac{1}{2} \end{aligned} $$
$$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-5 & =-\frac{1}{2}(x-4) \\ y & =-\frac{1}{2} x+2+5 \\ y & =-\frac{1}{2} x+7 \end{aligned} $$
(a)
$$ \text { Diagram } 3 \text { shows } \underline{a} \text { and } \stackrel{\rightharpoonup}{C D} \text { on a square grid. } $$
(i)$$ \text { Express } \stackrel{\rightharpoonup}{C D} \text { in terms of } \underline{a} \text {. } $$
(ii)
$$ \text { Draw }-4 \underline{a} \text { on Diagram } 3 . $$
[2 marks]
(b) Solutions by scale drawing and / or vector are not accepted.
Diagram 4 shows the straight line AB.
Given that point C lies on AB such that AC : CB = 2 : 1, find the coordinates of C.[2 marks]
(c) Solutions by scale drawing is not accepted.
It is given that P(4, 5) and Q(2, 1) line on a Cartesian plane.
Find the equation of the straight line which is perpendicular to the straight line PQ and passing through point P.
[3 marks]
Answer:
(a)(i)
$$ \begin{aligned} & \overrightarrow{C D}=\underline{a}+\underline{a}+\frac{1}{2} \underline{a} \\ & \overrightarrow{C D}=\frac{5}{2} \underline{a} \end{aligned} $$
(a)(ii)
(b)
$$ \begin{aligned} C(x, y) & =\left(\frac{2(-1)+(1)(5)}{2+1}, \frac{(2)(-1)+(1)(8)}{2+1}\right) \\ & =(1,2) \end{aligned} $$
(c)
$$ \begin{aligned} m_{P Q} & =\frac{5-1}{4-2} \\ & =2 \end{aligned} $$
$$ \begin{aligned} m_{P Q} \times m_2 & =-1 \\ 2 \times m_2 & =-1 \\ m_2 & =-\frac{1}{2} \end{aligned} $$
$$ \begin{aligned} y-y_1 & =m\left(x-x_1\right) \\ y-5 & =-\frac{1}{2}(x-4) \\ y & =-\frac{1}{2} x+2+5 \\ y & =-\frac{1}{2} x+7 \end{aligned} $$
Question 4:
Diagram 5 shows a circle with centre O and an arc AB which subtends an angle θ rad at O. It is given that the radius of the circle is r unit and the length of the minor arc AB is s unit.
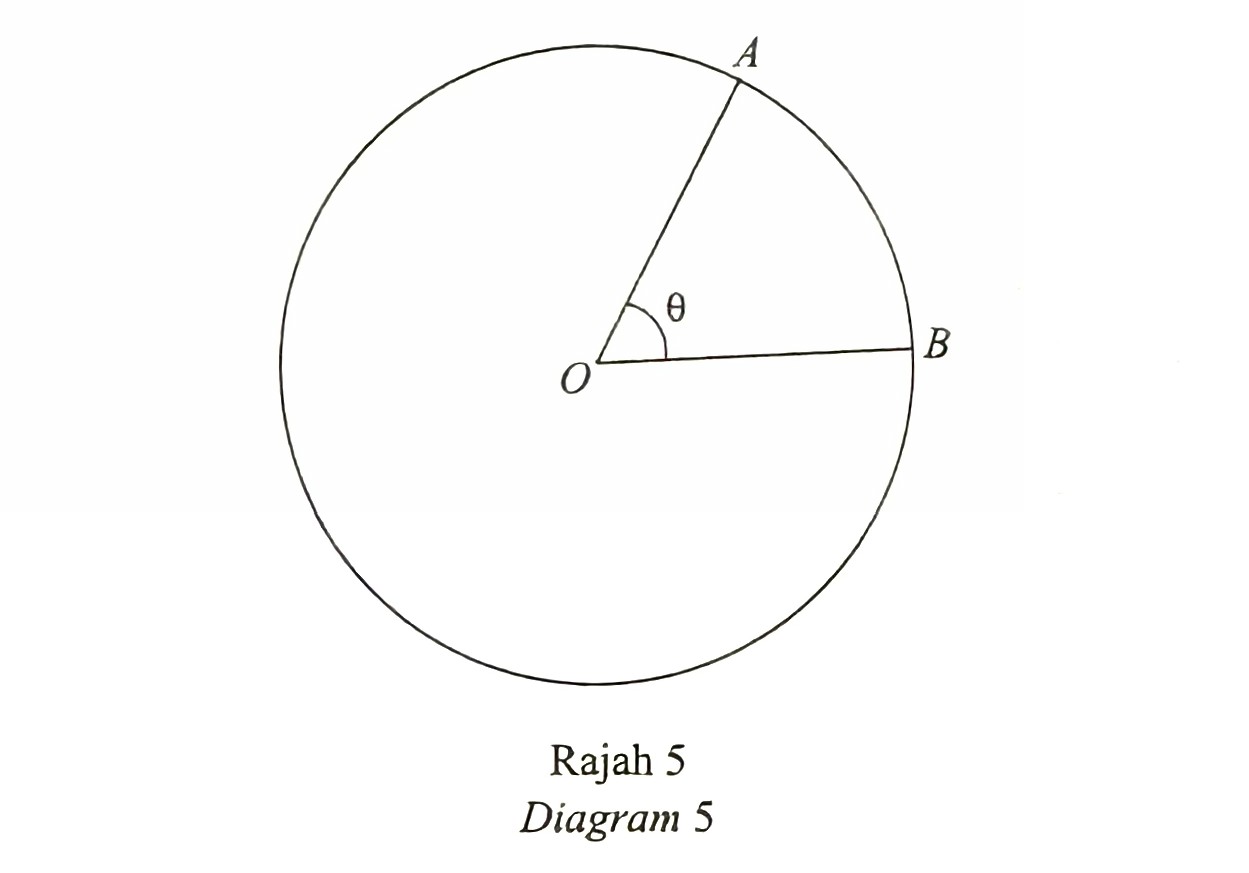
Based on Diagram 5, derive s = rθ.
[2 marks]
Answer:
$$ \begin{aligned} \frac{\text { Length of arc }}{\text { Circumference }} & =\frac{\text { Angle subtended at the centre }}{360^{\circ}} \\ \frac{s}{2 \pi r} & =\frac{\theta}{2 \pi} \\ s & =\frac{\theta}{2 \pi} \times 2 \pi r \\ s & =r \theta \end{aligned} $$
Diagram 5 shows a circle with centre O and an arc AB which subtends an angle θ rad at O. It is given that the radius of the circle is r unit and the length of the minor arc AB is s unit.
Based on Diagram 5, derive s = rθ.
[2 marks]
Answer:
$$ \begin{aligned} \frac{\text { Length of arc }}{\text { Circumference }} & =\frac{\text { Angle subtended at the centre }}{360^{\circ}} \\ \frac{s}{2 \pi r} & =\frac{\theta}{2 \pi} \\ s & =\frac{\theta}{2 \pi} \times 2 \pi r \\ s & =r \theta \end{aligned} $$