Question 1:
Diagram 1 shows the straight line graph obtained when y = 4x2 – 5 is reduced to linear form.
Express X and Y in terms of x and / or y. [2 marks]
Answer:
$$ \begin{aligned} & \left(y=4 x^2-5\right) \div x^2 \\ & \frac{y}{x^2}=4-\frac{5}{x^2} \\ & \frac{y}{x^2}=-5\left(\frac{1}{x^2}\right)+4 \\ & \boldsymbol{Y}=\boldsymbol{m} \quad \boldsymbol{X}+\boldsymbol{C} \\ & Y=\frac{y}{x^2} \\ & X=\frac{1}{x^2} \end{aligned} $$
Diagram 1 shows the straight line graph obtained when y = 4x2 – 5 is reduced to linear form.
Express X and Y in terms of x and / or y. [2 marks]
Answer:
$$ \begin{aligned} & \left(y=4 x^2-5\right) \div x^2 \\ & \frac{y}{x^2}=4-\frac{5}{x^2} \\ & \frac{y}{x^2}=-5\left(\frac{1}{x^2}\right)+4 \\ & \boldsymbol{Y}=\boldsymbol{m} \quad \boldsymbol{X}+\boldsymbol{C} \\ & Y=\frac{y}{x^2} \\ & X=\frac{1}{x^2} \end{aligned} $$
Question 2:
(a) Diagram 2 shows the relation of two sets.
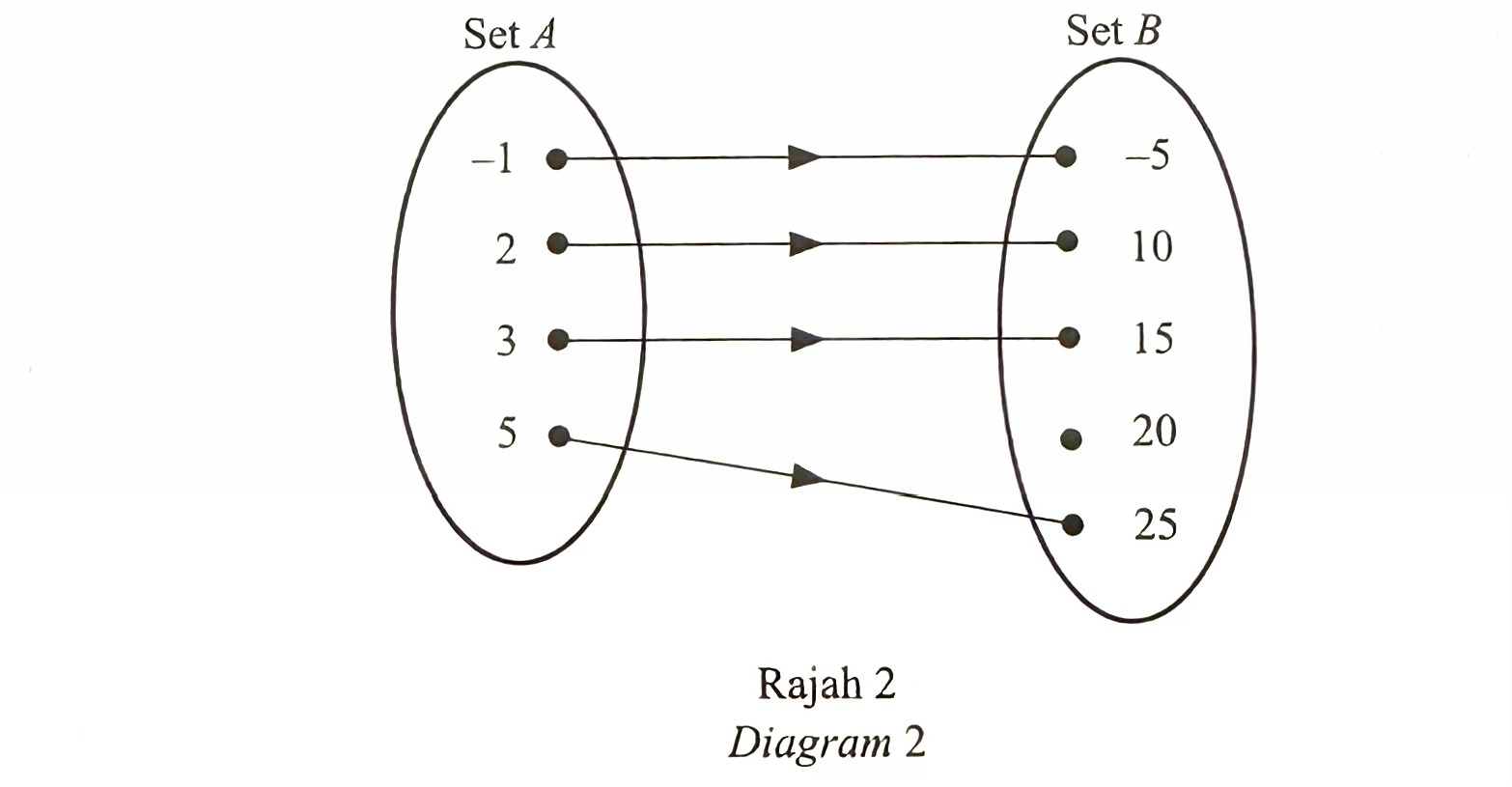
State the range of the relation. [1 mark]
(b) Function g(x) = 3 – x is expressed in the form of ordered pairs as below:
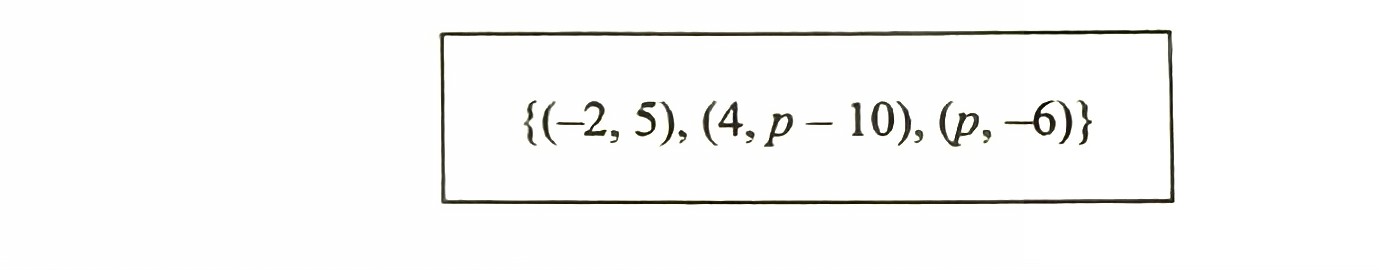Find the value of p.
[2 marks]
Answer:
(a) {-5, 10, 15, 25}
(b)
$$ \begin{aligned} g(x) & =3-x \\ g(4) & =p-10 \\ 3-4 & =p-10 \\ -1 & =p-10 \\ -1+10 & =p \\ p & =9 \end{aligned} $$
(a) Diagram 2 shows the relation of two sets.
State the range of the relation. [1 mark]
(b) Function g(x) = 3 – x is expressed in the form of ordered pairs as below:
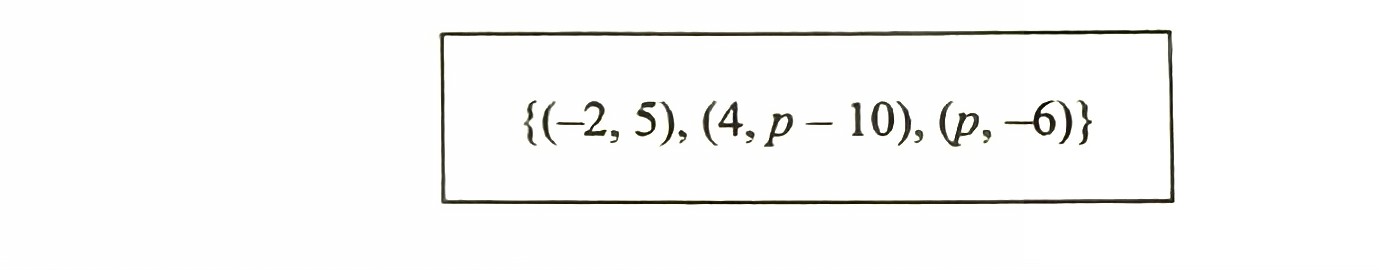Find the value of p.[2 marks]
Answer:
(a) {-5, 10, 15, 25}
(b)
$$ \begin{aligned} g(x) & =3-x \\ g(4) & =p-10 \\ 3-4 & =p-10 \\ -1 & =p-10 \\ -1+10 & =p \\ p & =9 \end{aligned} $$