3.6 Integration as the Summation of Volumes
(1).
(2).
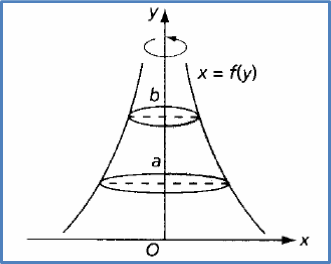
The volume of the solid generated when the region enclosed by the curve x = f(y), the y-axis, the line y = a and the line y = b is revolved through 360° about the y-axis is given by
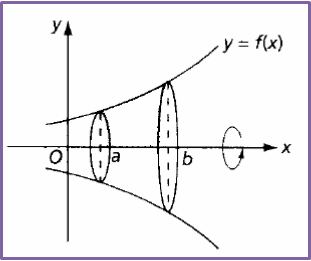
(1).

The volume of the solid generated when the region enclosed by the curve y = f(x), the x-axis, the line x = a and the line x = b is revolved through 360° about the x-axis is given by
(2).

The volume of the solid generated when the region enclosed by the curve x = f(y), the y-axis, the line y = a and the line y = b is revolved through 360° about the y-axis is given by
Example 1:
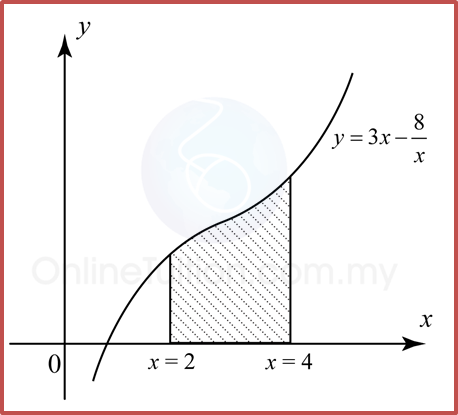
Solution:
Volume generated, Vx
Example 2:
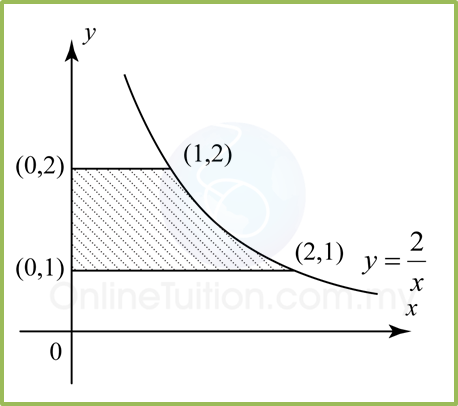
Solution:
Volume generated, Vy
Find the volume generated for the following diagram when the shaded region is revolved through 360° about the x-axis.

Solution:
Volume generated, Vx
Example 2:
Find the volume generated for the following diagram when the shaded region is revolved through 360° about the y-axis.

Volume generated, Vy