Question 7:
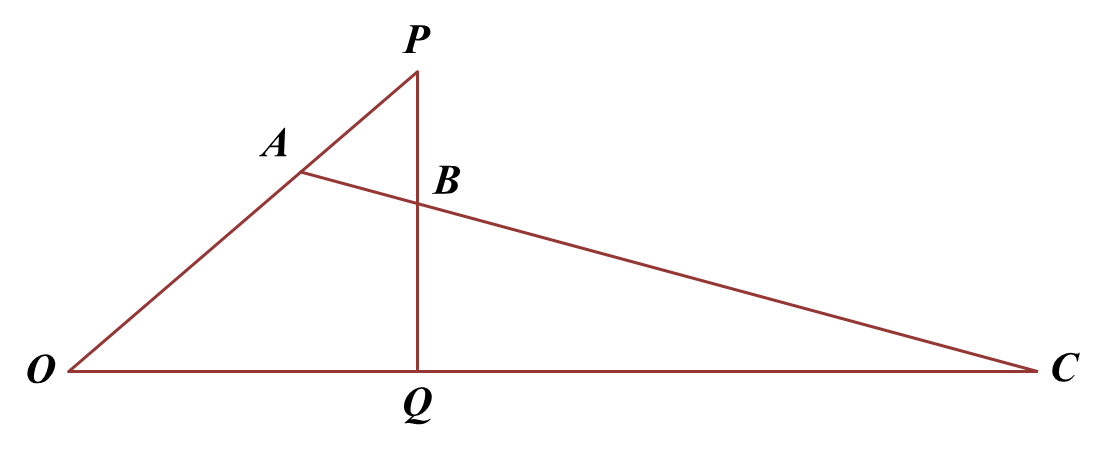
Diagram below shows quadrilateral
OPBC. The straight line
AC intersects the straight line
PQ at point
B.
Solution:
(a)
(b)
(c)(i)
(c)(ii)
Question 8:
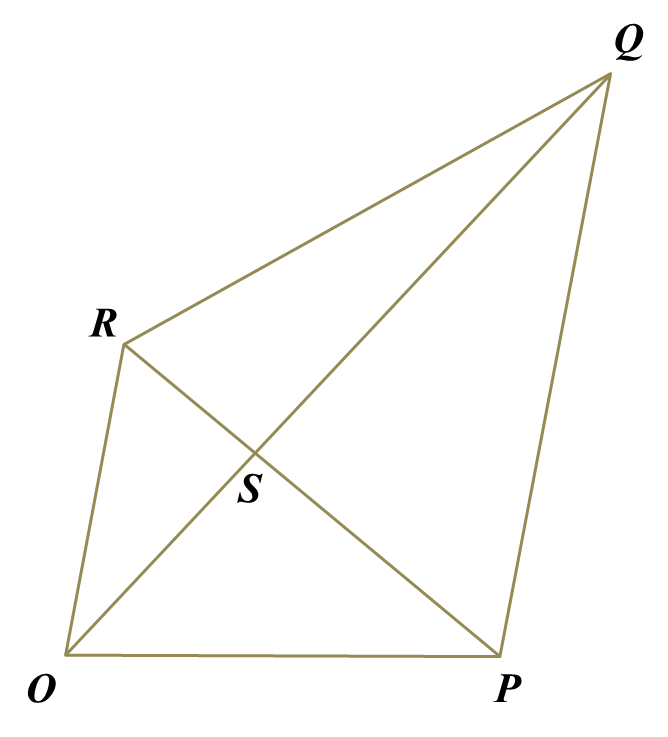
Diagram below shows quadrilateral
OPQR. The straight line
PR intersects the straight line
OQ at point
S.
Solution:
(a)(i)
(a)(ii)
(b)
(c)



