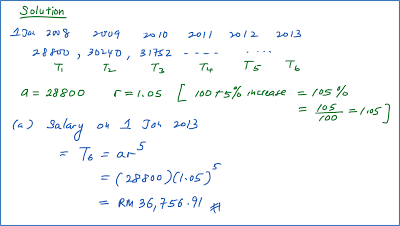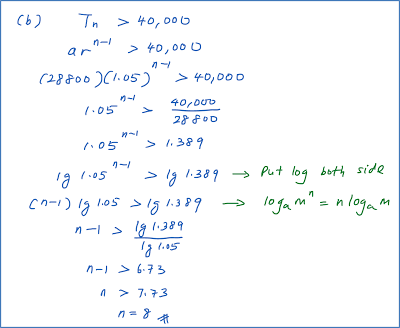Question 1:
Diagram below shows part of an arrangement of bricks of equal size.
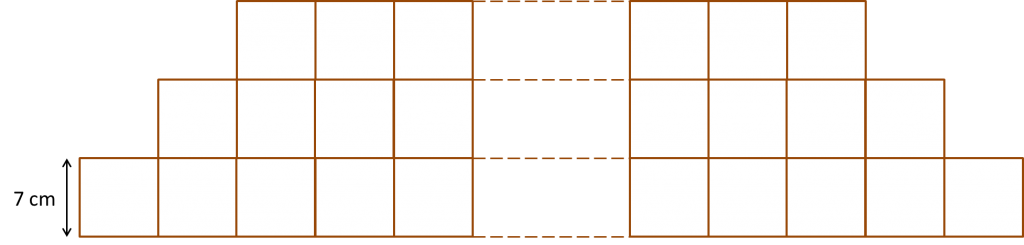
The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.
Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate
(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.
Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2
(a)
Tn = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm
(b)
Total number of bricks used
= S49
= 2548
Total price = 2548 × RM0.50
= RM1,274
Diagram below shows part of an arrangement of bricks of equal size.

The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.
Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate
(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.
Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2
(a)
Tn = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm
(b)
Total number of bricks used
= S49
= 2548
Total price = 2548 × RM0.50
= RM1,274
Question 2:
Mr Choong started working for a company on 1 January 2008 with an initial annual salary of RM28800. Every January, the company increased his salary by 5% of the previous year’s salary.
Calculate
(a) his annual salary, to the nearest RM on 1 January 2013,
(b) the minimum value of n such that his annual salary in the nth year will exceed RM40 000,
(c) the total salary, to the nearest RM, paid to him by the company, for the years 2008 to 2013.
Solution:

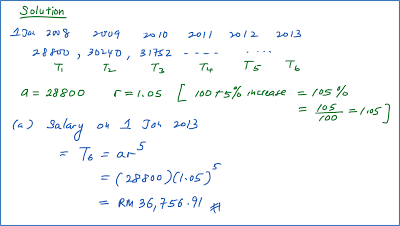
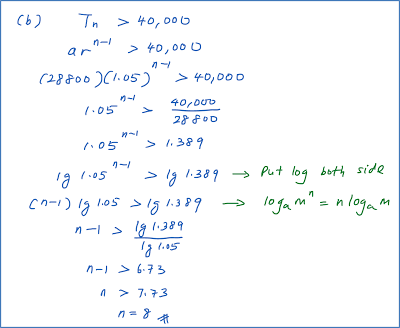

Mr Choong started working for a company on 1 January 2008 with an initial annual salary of RM28800. Every January, the company increased his salary by 5% of the previous year’s salary.
Calculate
(a) his annual salary, to the nearest RM on 1 January 2013,
(b) the minimum value of n such that his annual salary in the nth year will exceed RM40 000,
(c) the total salary, to the nearest RM, paid to him by the company, for the years 2008 to 2013.
Solution: