Question 6:
Find the number of the multiples of 8 between 100 and 300.
Solution:

Find the number of the multiples of 8 between 100 and 300.
Solution:

Question 7:
Find the sum of all the multiples of 7 between 100 and 500.
Solution:

Find the sum of all the multiples of 7 between 100 and 500.
Solution:

Question 8:
If are the first three terms of a progression, show that it forms an arithmetic progression.
Solution:

If are the first three terms of a progression, show that it forms an arithmetic progression.
Solution:

Question 9:
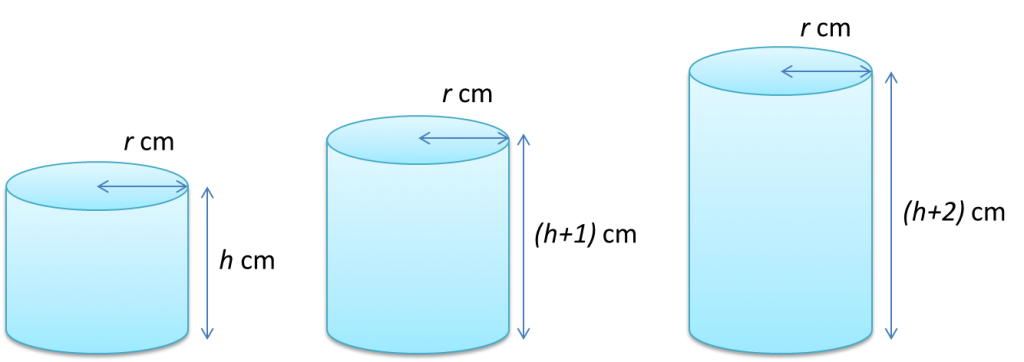
Show that the volumes of the cylinders in the above diagram form an arithmetic progression and state its common difference.
Solution:


Show that the volumes of the cylinders in the above diagram form an arithmetic progression and state its common difference.
Solution:

Question 10:
The sequence –11, –5, 1,… is an arithmetic progression. State the three consecutive terms of this arithmetic progression where the sum of these three terms is 93.
Solution:

The sequence –11, –5, 1,… is an arithmetic progression. State the three consecutive terms of this arithmetic progression where the sum of these three terms is 93.
Solution:

i cant open the next aritmetic progressions