Question 4:
Solution:
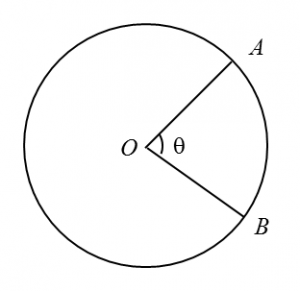
Diagram below shows a circle with centre O.

The length of the minor arc is 16 cm and the angle of the major sector AOB is 290o.
Using π = 3.142, find
(a) the value of θ, in radians. (Give your answer correct to four significant figures)
(b) the length, in cm, of the radius of the circle.
(a)
Angle of the minor sector AOB
= 360o – 290o
= 70o
= 70o ×
= 1.222 radians
(b)
Using s = rθ
r × 1.222 = 16
radius, r = 13.09 cm
Question 5:
Solution:
(a) s = r θ
Diagram below shows sector OPQ with centre O and sector PXY with centre P.
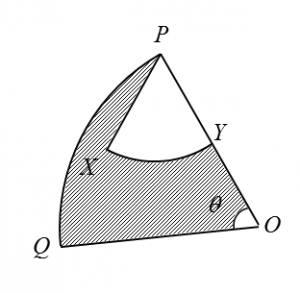 Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
 Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,
Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,calculate
( a) the value of θ , in radian ,
( b) the area, in cm2 , of the shaded region .
(a) s = r θ
6 = 8 θ
θ = 0.75 rad
(b)
Area of the shaded region
= Area of sector OPQ – Area of sector PXY
= 24 – 5.4
= 18.6 cm2
Question 6:
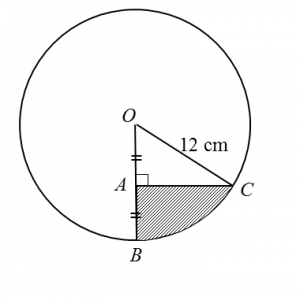 Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Solution:
Diagram below shows a circle with centre O and radius 12 cm.
 Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find
Given that A, B and C are points such that OA = AB and ∠OAC = 90°, find(a) ∠BOC, in radians,
(b) the area, in cm2, of the shaded region.
(a) For triangle OAC,
cos ∠AOC = 6/12
ÐAOC = 1.047 rad (change calculator to Rad mode)
ÐBOC = 1.047 rad
(b)
Area of the shaded region
= Area of BOC – Area of triangle AOC
= ½ (12)2 (1.047) – ½ (6) (12) sin 1.047 (change calculator to Rad mode)
= 75.38 – 31.17
= 44.21 cm2