Question 5:
Solution:
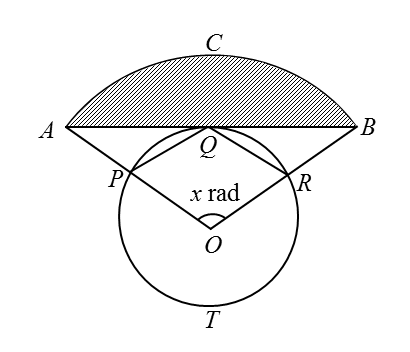
Diagram below shows a circle PQRT, centre O and radius 5 cm. AQB is a tangent to the circle at Q. The straight lines, AO and BO, intersect the circle at P and R respectively.
OPQR is a rhombus. ACB is an arc of a circle at centre O.
 Calculate
Calculate
 Calculate
Calculate(a) the angle x , in terms of π ,
(b) the length , in cm , of the arc ACB ,
(c) the area, in cm2,of the shaded region.
Solution:
(a)
Rhombus has 4 equal sides, therefore OP = PQ = QR = OR = 5 cm
OR is radius to the circle, therefore OR = OQ = 5 cm
Triangles OQR and OQP are equilateral triangle,
Therefore, ∠ QOR= ∠QOP = 60o
∠ POR = 120o
x = 120o × π/180o
x = 2π/ 3 rad
(b)
cos ∠ AOQ= OQ / OA
cos 60o = 5 / OA
OA = 10 cm
Length of arc, ACB,
s = r θ
Arc ACB = (10) (2π / 3)
Arc ACB = 20.94 cm
(c)
Question 6:
Solution:
(a)
(b)
(c)

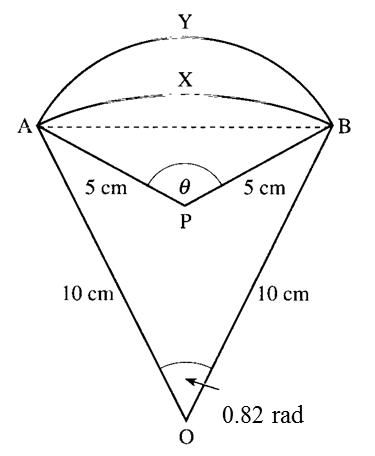
In the diagram above, AXB is an arc of a circle centre O and radius 10 cm with ∠AOB = 0.82 radian. AYB is an arc of a circle centre P and radius 5 cm with ∠APB = θ.
Calculate:
Calculate:
(a) the length of the chord AB,
(b) the value of θ in radians,
(c) the difference in length between the arcs AYB and AXB.
Solution:
(a)
(b)
(c)
Using s = rθ
Arcs AXB = 10 × 0.82 = 8.2 cm
Arcs AYB = 5 × 1.848 = 9.24 cm
Difference in length between the arcs AYB and AXB
= 9.24 – 8.2
= 1.04 cm