\

1.3 Area of a Sector of a Circle

1.3 Area of a Sector of a Circle
(A) Area of a Sector of a Circle

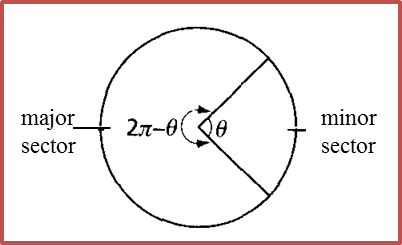
1. If a circle divided into two sectors of different sizes, the smaller sector is known as the minor sector while the larger sector is known as the major sector.



2. If AOB is the area of a sector of a circle, of radius r, that subtends an angle θ radians, at the centre O, then




Example 1:
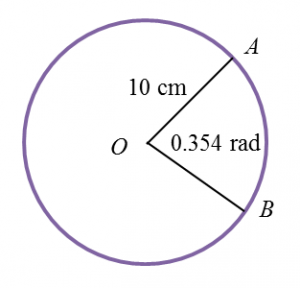
In the above diagram, find the area of the sector OAB.

Solution:
Area of the sector OAB
= 1 2 r 2 θ = 1 2 ( 10 ) 2 ( 0.354 ) = 17.7  cm 2


(B) To Calculate the Area of a Segment of a Circle



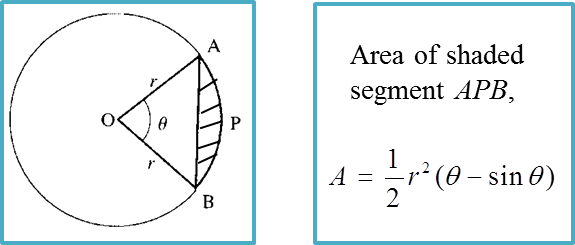
Example 2:


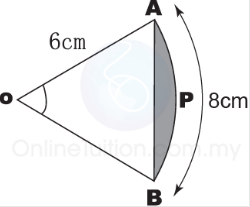
The above diagram shows a sector of a circle, with centre O and a radius 6 cm. The length of the arc AB is 8 cm. Find
(i) ∠AOB
(ii) the area of the shaded segment.


Solution:
(i) Length of the arc AB = 8 cm
rθ = 8
6θ = 8
θ = 1.333 radians
∠AOB = 1.333 radians

(ii)
the area of the shaded segment
= 1 2 r 2 ( θ − sin θ ) = 1 2 ( 6 ) 2 ( 1.333 − sin 1.333 r ) = 1 2 ( 36 ) ( 1.333 − 0.972 ) = 6.498  cm 2

Leave a Comment