Question 13 (10 marks):
Table 2 shows the prices and the price indices of three types of ingredients P, Q and R, used in the production of a type of instant noodle.
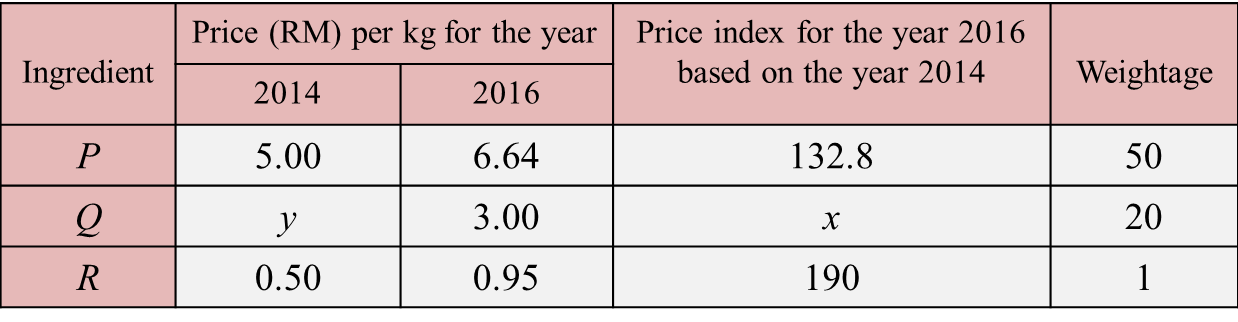
(a) The price of ingredient Q increased by 20% from the year 2014 to the year 2016.
(i) State the value of x.
(ii) Find the value of y.
(b) Calculate the composite index for the cost of making the instant noodles for the year 2016 based on the year 2014.
(c) It is given that the composite index for the cost of making the instant noodles increased by 40% from the year 2012 to the year 2016.
(i) Calculate the composite index for the cost of making the instant noodles in the year 2014 based on the year 2012.
(ii) The cost of making a packet of instant noodle is 10 sen in the year 2012.
Find the maximum number of packet of instant noodles that can be produced using an allocation of RM80 in the year 2016.
Solution:
(a)(i)
x = 120
(a)(ii)
(b)
(c)(i)
(c)(ii)
Table 2 shows the prices and the price indices of three types of ingredients P, Q and R, used in the production of a type of instant noodle.

(a) The price of ingredient Q increased by 20% from the year 2014 to the year 2016.
(i) State the value of x.
(ii) Find the value of y.
(b) Calculate the composite index for the cost of making the instant noodles for the year 2016 based on the year 2014.
(c) It is given that the composite index for the cost of making the instant noodles increased by 40% from the year 2012 to the year 2016.
(i) Calculate the composite index for the cost of making the instant noodles in the year 2014 based on the year 2012.
(ii) The cost of making a packet of instant noodle is 10 sen in the year 2012.
Find the maximum number of packet of instant noodles that can be produced using an allocation of RM80 in the year 2016.
Solution:
(a)(i)
x = 120
(a)(ii)
(b)
(c)(i)
(c)(ii)
Question 15 (10 marks):
Solution by scale drawing is not accepted.
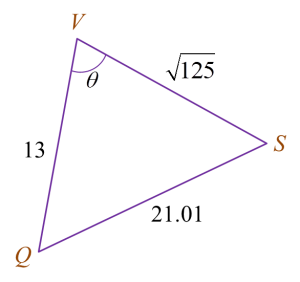
Diagram 8 shows a quadrilateral PQRS on a horizontal plane.
 VQSP is a pyramid such that PQ = 12 m and V is 5 m vertically above P.
VQSP is a pyramid such that PQ = 12 m and V is 5 m vertically above P.
Find
(a) ∠QSR,
(b) the length, in m, of QS,
(c) the area, in m2, of inclined plane QVS.
Solution:
(a)
(b)
(c)
Solution by scale drawing is not accepted.
Diagram 8 shows a quadrilateral PQRS on a horizontal plane.
 VQSP is a pyramid such that PQ = 12 m and V is 5 m vertically above P.
VQSP is a pyramid such that PQ = 12 m and V is 5 m vertically above P.Find
(a) ∠QSR,
(b) the length, in m, of QS,
(c) the area, in m2, of inclined plane QVS.
Solution:
(a)
(b)
(c)
