5.2c Probability of an Event
Example:
The masses of pears in a fruit stall are normally distributed with a mean of 220 g and a variance of 100 g. Find the probability that a pear that is picked at random has a mass
(a) of more than 230 g.
(b) between 210 g and 225 g.
Hence, find the value of h such that 90% of the pears weigh more than h g.
Solution:
µ = 220 g
σ = √100 = 10 g
Let X be the mass of a pear.
(a)
(b)
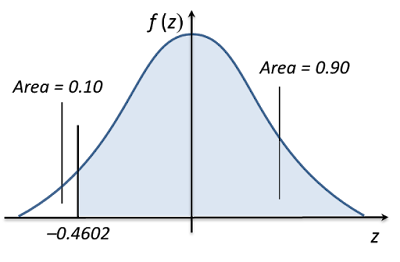
For 90% (probability = 0.9) of the pears weigh more than h g,
P (X > h) = 0.9
P (X < h) = 1 – 0.9
= 0.1
From the standard normal distribution table,
P (Z > 0.4602) = 0.1
P (Z < –0.4602) = 0.1