Question 3:
The masses of mangoes in a stall have a normal distribution with a mean of 200 g and a standard deviation of 30 g.
(a) Find the mass, in g, of a mango whose z-score is 0.5.
(b) If a mango is chosen at random, find the probability that the mango has a mass of at least 194 g.
Solution:
µ = 200 g
σ = 30 g
Let X be the mass of a mango.
(a)
(b)
Question 4:
Diagram below shows a standard normal distribution graph.
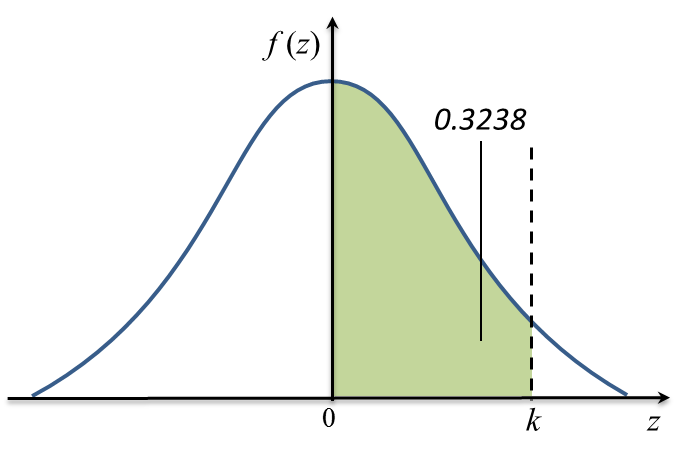

The probability represented by the area of the shaded region is 0.3238.
(a) Find the value of k.
(b) X is a continuous random variable which is normally distributed with a mean of 80 and variance of 9.
Find the value of X when the z-score is k.
Solution:
(a)
P(Z > k) = 0.5 – 0.3238
= 0.1762
k = 0.93
(b)
µ = 80,
σ2 = 9, σ = 3