Question 5:
Solution:
Lisa has a rectangular plot of land. She plants orchid and rears fish in the areas as shown on diagram above. The area used for planting orchid is 460 m2 and the perimeter of the rectangular fish pond is 48 m. Find the value of x and y.
Solution:
Area used for planting orchid = 460 m2
10 (30 – y) + xy = 460
300 – 10y + xy = 460
xy – 10y = 160
y (x – 10) = 160
Perimeter of the rectangular fish pond = 48 m
2 (x – 10) + 2 (30 – y) = 48
2x – 20 + 60 – 2y = 48
2x – 2y= 8
x – y = 4
x = 4 + y —— (2)x – y = 4
Substitute (2) into (1):
From (2),
When y = 16
x = 4 + 16 = 20
Question 6:
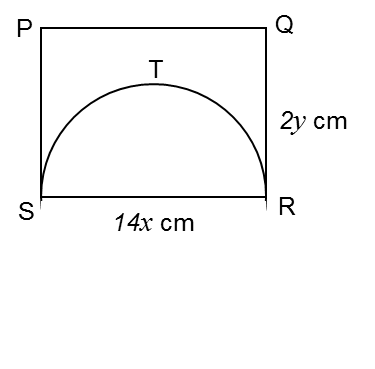
In the diagram above, PQRS is a rectangular piece of paper with an area of 112 cm2. A semicircle STR is cut from this piece of paper. The perimeter of the remaining piece of paper is 52 cm. Using , find the integer value of x and y.
Solution:
In the diagram above, PQRS is a rectangular piece of paper with an area of 112 cm2. A semicircle STR is cut from this piece of paper. The perimeter of the remaining piece of paper is 52 cm. Using , find the integer value of x and y.
Solution:
Area of the rectangle PQRS = 112 cm2
Therefore, (14x)(2y) = 112
28xy= 112
xy = 4 —— (1)
Perimeter of PSTRQ = 52 cm
PS + QR + PQ + Length of arc STR = 52
2y + 2y + 14x + ½ (2πr) = 52
4y + 14x +
= 52
4y + 14x + 22x = 52
4y + 36x = 52
y + 9x = 13 —— (2)
From equation (2) : y = 13 – 9x —— (3)
Substitute (3) into (1) :
x (13 – 9x) = 4
13x – 9x2 = 4
9x2 – 13x + 4 = 0
(x – 1)(9x – 4) = 0
x = 1 or
From (3) :
When x = 1,
y = 13 – 9(1) = 4.