Question 7:
It is given that
, where A is an obtuse angle and B is an acute angle.
Find
(a) tan A
(b) sin (A + B)
(c) cos (A – B)
Solution:
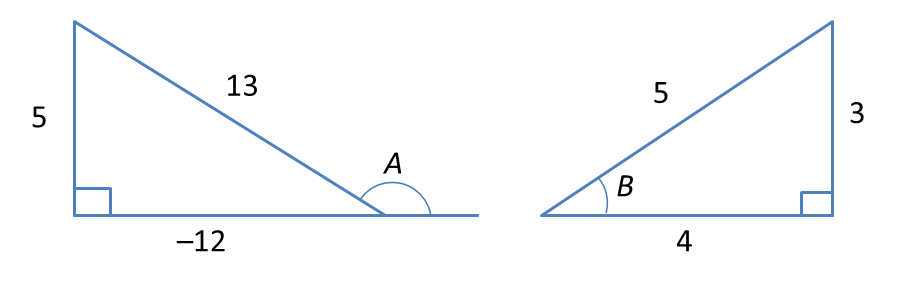 (a)
(b)
(c)
(a)
(b)
(c)
Question 8:
If sin A = p, and 90° < A < 180°, express in terms of p
(a) tan A
(b) cos A
(c) sin 2A
Solution:
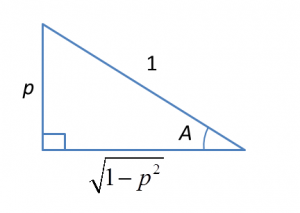
(a)
(b)
(c)
 (a)
(a) (a)
(a)
