Question 6:
Solution:
(a)
(b)
(c)

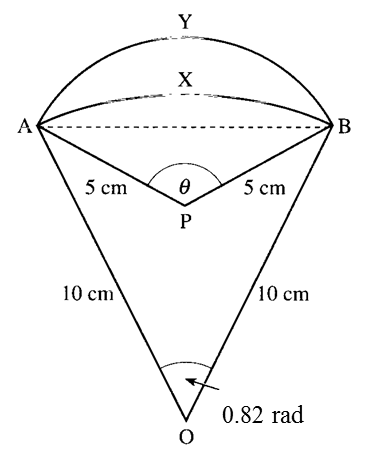
In the diagram above, AXB is an arc of a circle centre O and radius 10 cm with ∠AOB = 0.82 radian. AYB is an arc of a circle centre P and radius 5 cm with ∠APB = θ.
Calculate:
Calculate:
(a) the length of the chord AB,
(b) the value of θ in radians,
(c) the difference in length between the arcs AYB and AXB.
Solution:
(a)
(b)
(c)
Using s = rθ
Arcs AXB = 10 × 0.82 = 8.2 cm
Arcs AYB = 5 × 1.848 = 9.24 cm
Difference in length between the arcs AYB and AXB
= 9.24 – 8.2
= 1.04 cm
Question 7:
Diagram below shows a semicircle PTS, centre O and radius 8 cm. PTR is a sector of a circle with centre P and Q is the midpoint of OS.
 [Use π = 3.142]
[Use π = 3.142]
Calculate
(a) ∠TOQ, in radians,
(b) the length , in cm , of the arc TR ,
(c) the area, in cm2 ,of the shaded region.
Solution:
(a)
(b)

(c)
Diagram below shows a semicircle PTS, centre O and radius 8 cm. PTR is a sector of a circle with centre P and Q is the midpoint of OS.
 [Use π = 3.142]
[Use π = 3.142]Calculate
(a) ∠TOQ, in radians,
(b) the length , in cm , of the arc TR ,
(c) the area, in cm2 ,of the shaded region.
Solution:
(a)
(b)

(c)
Question 8:
Diagram below shows a circle PQT with centre O and radius 7 cm.

QS is a tangent to the circle at point Q and QSR is a quadrant of a circle with centre Q. Q is the midpoint of OR and QP is a chord. OQR and SOP are straight lines.
[Use π = 3.142]
Calculate
(a) angle θ, in radians,
(b) the perimeter, in cm ,of the shaded region,
(c) the area, in cm2 ,of the shaded region.
Solution:
(a)
(b)
(c)
Diagram below shows a circle PQT with centre O and radius 7 cm.

QS is a tangent to the circle at point Q and QSR is a quadrant of a circle with centre Q. Q is the midpoint of OR and QP is a chord. OQR and SOP are straight lines.
[Use π = 3.142]
Calculate
(a) angle θ, in radians,
(b) the perimeter, in cm ,of the shaded region,
(c) the area, in cm2 ,of the shaded region.
Solution:
(a)
(b)
(c)
Question 9:
In diagram 5, AOBDE, is a semicircle with centre O and has radius of 5cm. ABC is a right angle triangle.
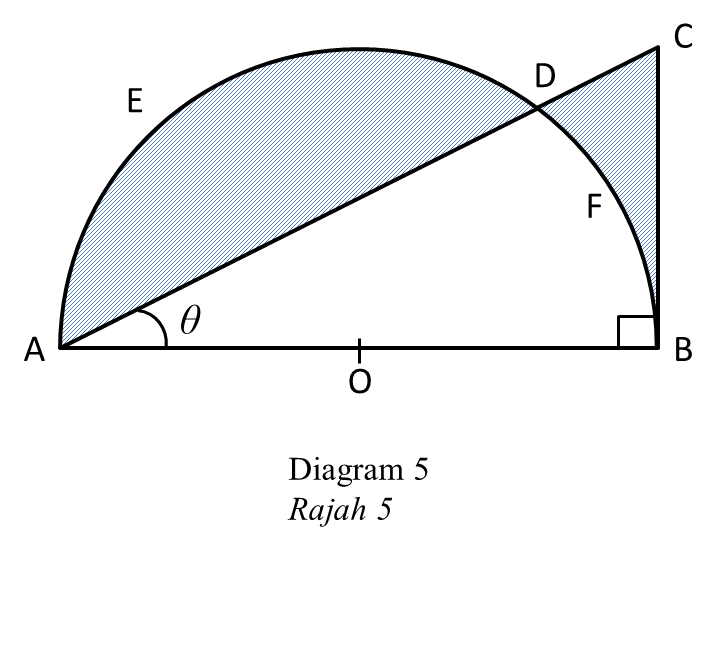

It is given that
[Use π = 3.142]
Calculate
(a) the value of θ, in radians, [2 marks]
(b) the perimeter, in cm, of the segment ADE, [3 marks]
(c) the area, in cm2, of the shaded region BCDF. [5 marks]Solution:
(a)
(b)
∠AOD = 3.142 – (0.4678 × 2)
= 2.206 rad
Length of arc AED = 5 × 2.206
= 11.03 cm
Therefore, perimeter of the segment ADE
= 11.03 + 8.8935
= 19.924 cm
(c)
BC = √ AC2 – AB2
= √11.20352 – 102
= 5.052 cm
Question 10 (SPM 2017 - 8 marks):
Diagram 1 shows a circle and a sector of a circle with a common centre O. The radius of the circle is r cm.
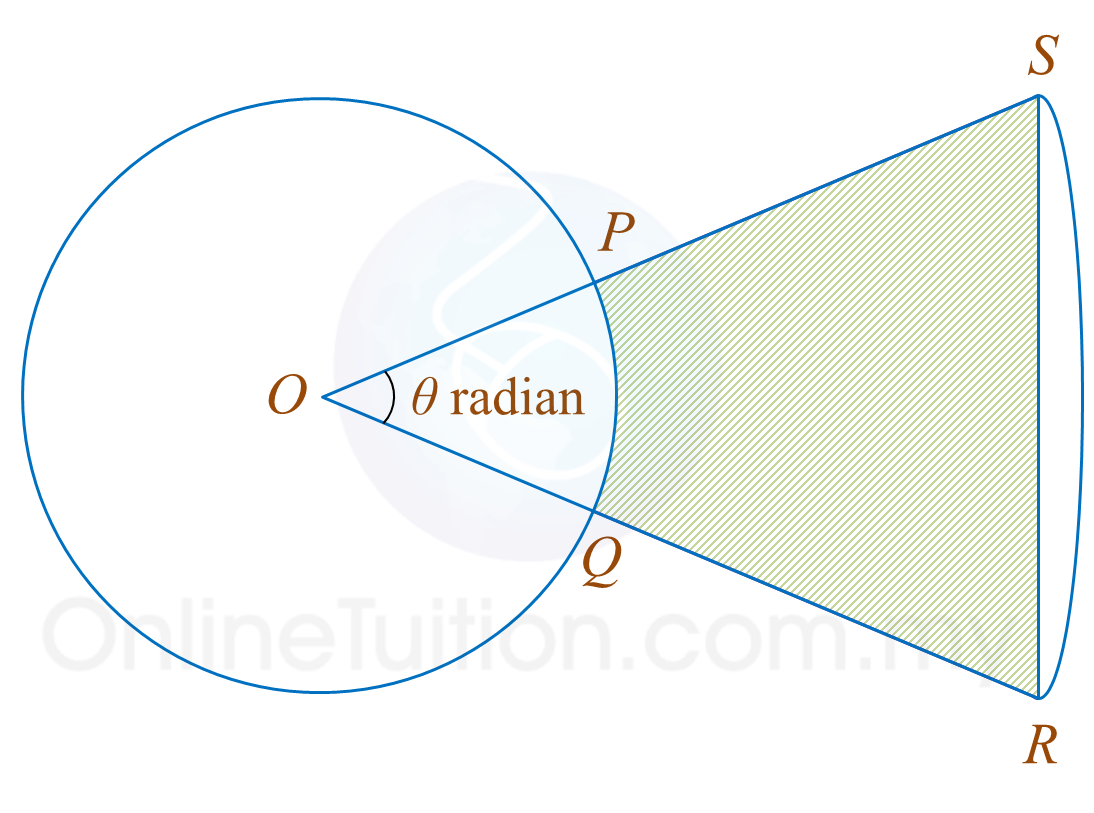
It is given that the length of arc PQ and arc RS are 2 cm and 7 cm respectively. QR = 10 cm.
[Use θ = 3.142]
Find
(a) the value of r and of θ,
(b) the area, in cm2, of the shaded region.
Solution:
(a)
(b)
Diagram 1 shows a circle and a sector of a circle with a common centre O. The radius of the circle is r cm.

It is given that the length of arc PQ and arc RS are 2 cm and 7 cm respectively. QR = 10 cm.
[Use θ = 3.142]
Find
(a) the value of r and of θ,
(b) the area, in cm2, of the shaded region.
Solution:
(a)
(b)