Question 1:
Solution:
(a)
(b)
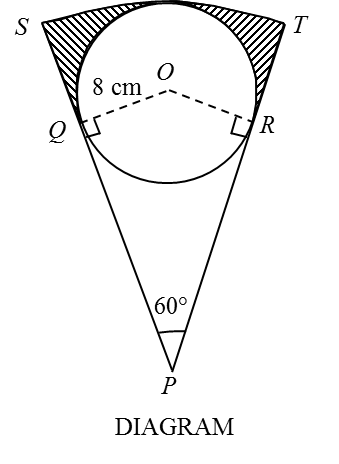
Diagram shows a circle, centre O and radius 8 cm inscribed in a sector SPT of a circle at centre P. The straight lines, SP and TP, are tangents to the circle at point Q and point R, respectively.
[Use p= 3.142]
Calculate
(a) the length, in cm, of the arc ST,
(b) the area, in cm2, of the shaded region.
Solution:
(a)
(b)
Question 2:
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.
 [Use π = 3.142]
[Use π = 3.142]
Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm2, of the shaded region.
Solution:
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.
 [Use π = 3.142]
[Use π = 3.142]Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm2, of the shaded region.
Solution:
this website was really useful .are there any harder questions? thanks.