Question 1:
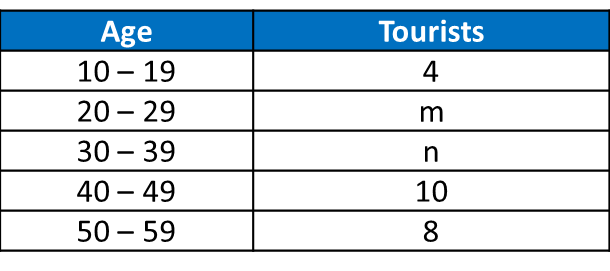
Given that the median age is 35.5, find the value of m and of n.
Solution:
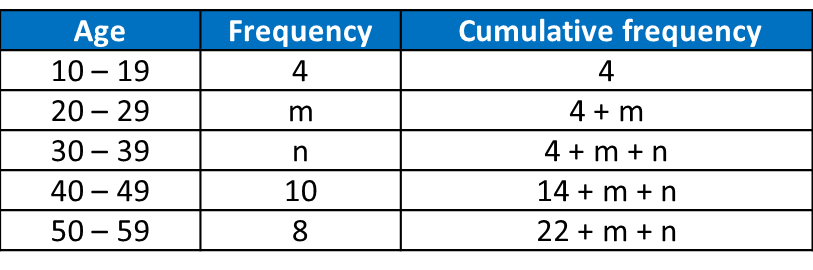
Table shows the age of 40 tourists who visited a tourist spot.

Given that the median age is 35.5, find the value of m and of n.
Given that the median age is 35.5, find the value of m and of n.

22 + m + n = 40
n = 18 – m —–(1)
Given median age = 35.5, therefore median class = 30 – 39
6n = 160 – 10m
3n = 80 – 5m —–(2)
Substitute (1) into (2).
3 (18 – m) = 80 – 5m
54 – 3m = 80 – 5m
2m = 26
m = 13
Substitute m = 13 into (1).
n = 18 – 13
n = 5
Thus m = 13, n = 5.
Question 2:
(b) Each mark is multiplied by 2 and then 3 is added to it.
Solution:
(a)(i)
(a)(ii)
(b)(i)
A set of examination marks x1, x2, x3, x4, x5, x6 has a mean of 6 and a standard deviation of 2.4.
(a) Find
(i) the sum of the marks,
,
(ii) the sum of the squares of the marks,
.
(b) Each mark is multiplied by 2 and then 3 is added to it.
Find, for the new set of marks,
(i) the mean,
(ii) the variance.
(a)(i)
(a)(ii)
(b)(i)
Mean of the new set of numbers
= 6(2) + 3
= 15
(b)(ii)
Variance of the original set of numbers
= 2.42 = 5.76
Variance of the new set of numbers
= 22 (5.76)
= 23.04