(A) Formulae for Length and Area of a Circle

r = radius, A= area, s = arc length, q = angle, l = length of chord
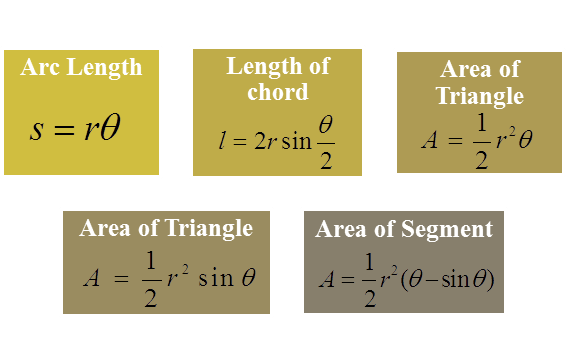
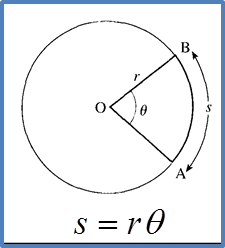
(B) Length of an Arc of a Circle
Example 1:
An arc, AB, of a circle of radius 5 cm subtends an angle of 1.5 radians at the centre. Find the length of the arc AB.
Solution:
Example 3:

Example 1:
An arc, AB, of a circle of radius 5 cm subtends an angle of 1.5 radians at the centre. Find the length of the arc AB.
Solution:
s = rθ
Length of the arc AB = (5)(1.5) = 7.5 cm
Example 2:
An arc, PQ, of a circle of radius 12 cm subtends an angle of 30° at the centre. Find the length of the arc PQ.
Solution:
Solution:
Length of the arc PQ
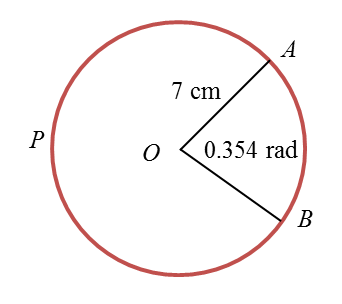
Example 3:

In the above diagram, find
(i) length of the minor arc AB
(ii) length of the major arc APB
Solution:
(i) length of the minor arc AB = rθ
= (7)(0.354)
= 2.478 cm
(ii) Since 360o = 2π radians, the reflex angle AOB
= (2π – 0.354) radians.
Length of the major arc APB
= 7 × (2π – 0.354)
= 7 × [(2)(3.1416) – 0.354]
= 7 × 5.9292
= 41.5044 cm
This is truly helpful, thanks.
really helpful to me Thanks for giving definition