7.1 Distance between Two Points
A (x1, y1) and C (x2, y2) are two points on a coordinate plane as shown below. BC is parallel to the x-axis and AB is parallel to the y-axis. Hence ∆ ABC = 90°.
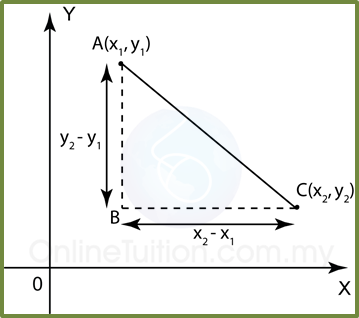
Distance between Point A and C =

Example:
Find the distance between the points P (2, –2) and Q (–4, –5).
Solution:
Let P (2, –2) = (x1, y1 ) and Q (–4, –5) = (x2, y2 ).