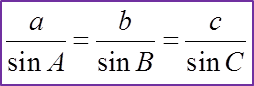\

9.1 The Sine Rule

9.1 The Sine Rule
In a triangle ABC in which the sides BC, CA and AB are denoted by a, b, and c as shown, and A, B, C are used to denote the angles at the vertices A, B, C respectively,



The sine rule can be used when
(i) two sides and one non-included angle or
(ii) two angles and one opposite side are given.


(A) If you know 2 angles and 1 side ⇒ Sine rule

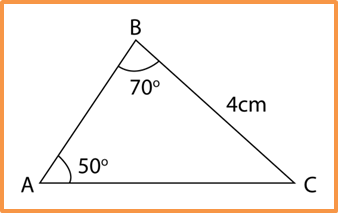
Example:


Calculate the length, in cm, of AB.

Solution:
∠ACB = 180o – (50o + 70o) = 60o
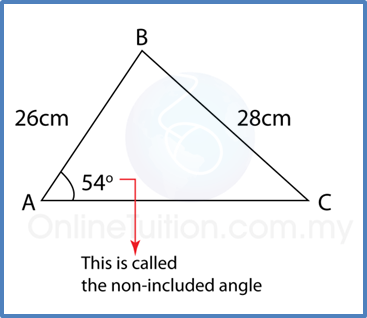
A B sin 60 o = 4 sin 50 o A B = 4 × sin 60 o sin 50 o A B = 4.522  cm

(B) If you know 2 sides and 1 angle (but not between them) ⇒ Sine rule

Example:

Calculate ∠ACB.

Solution:
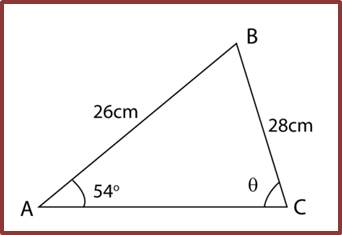
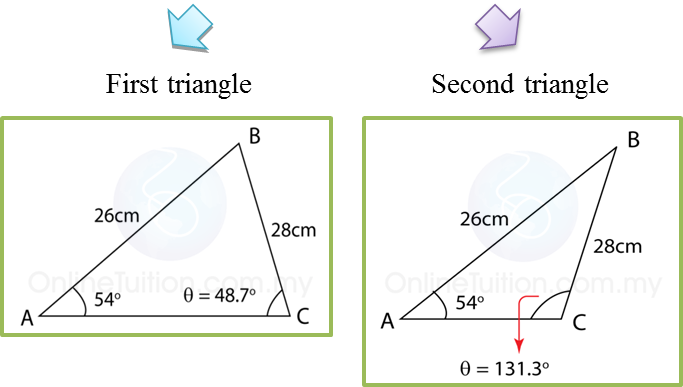
28 sin 54 o = 26 sin ∠ A C B sin ∠ A C B = 26 × sin 54 o 28 sin ∠ A C B = 0.7512 ∠ A C B = 48.7 o

(C) Case of ambiguity (2 possible triangles)

Example

Calculate ∠ACB, θ.

Solution:
Two possible triangle with these measurement
AB = 26cm BC = 28 cm Ð BAC = 54o
26 sin θ = 28 sin 54 o sin θ = 0.7512 θ = sin − 1 0.7512 θ = 48.7 o , 180 o − 48.7 o θ = 48.7 o  (Acute angle) ,   131.3 o  (Obtuse angle)

Leave a Comment