Question 6:
The first three terms of a sequence are 2, x, 18. Find the positive value of x so that the sequence is
(a) an arithmetic progression,
(b) a geometric progression.
Solution:
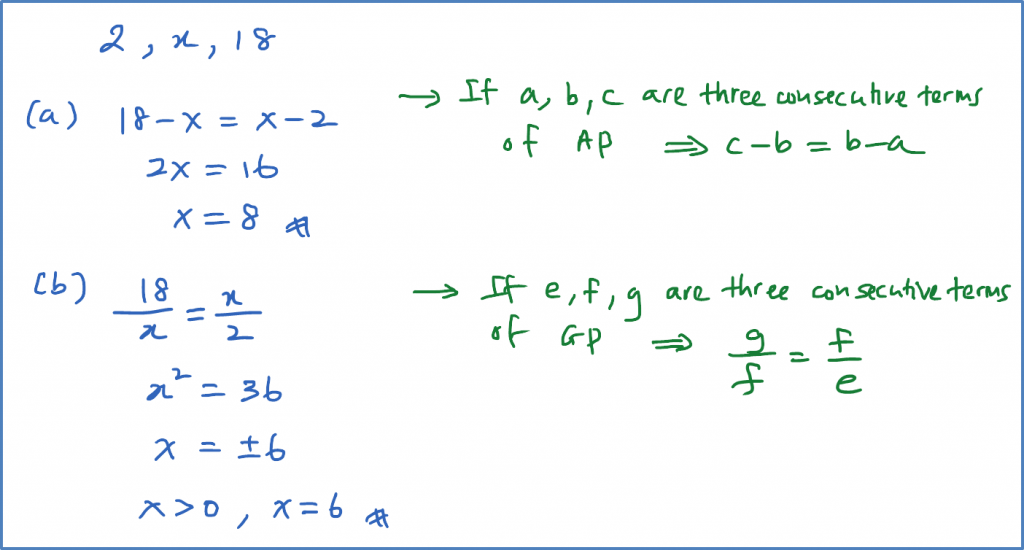
The first three terms of a sequence are 2, x, 18. Find the positive value of x so that the sequence is
(a) an arithmetic progression,
(b) a geometric progression.
Solution:
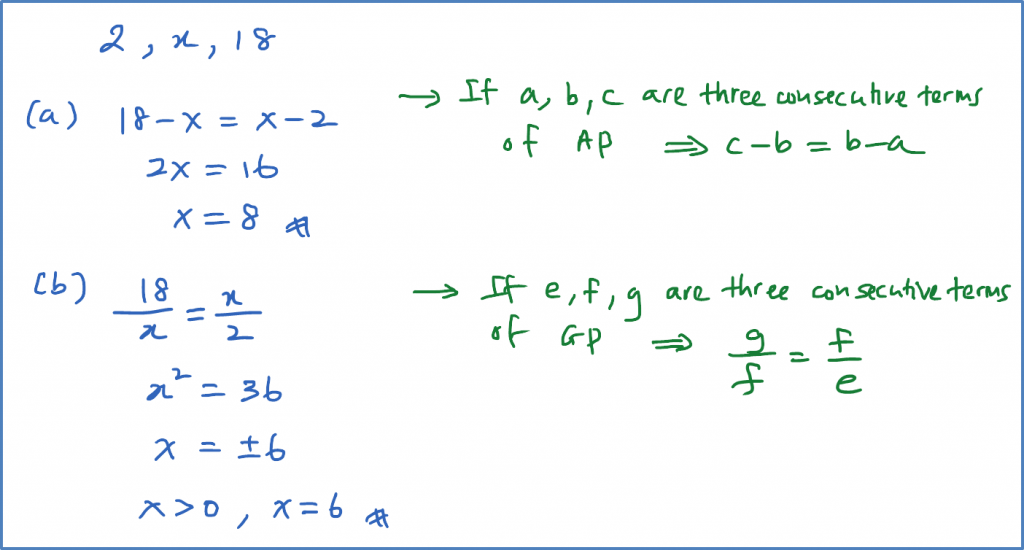
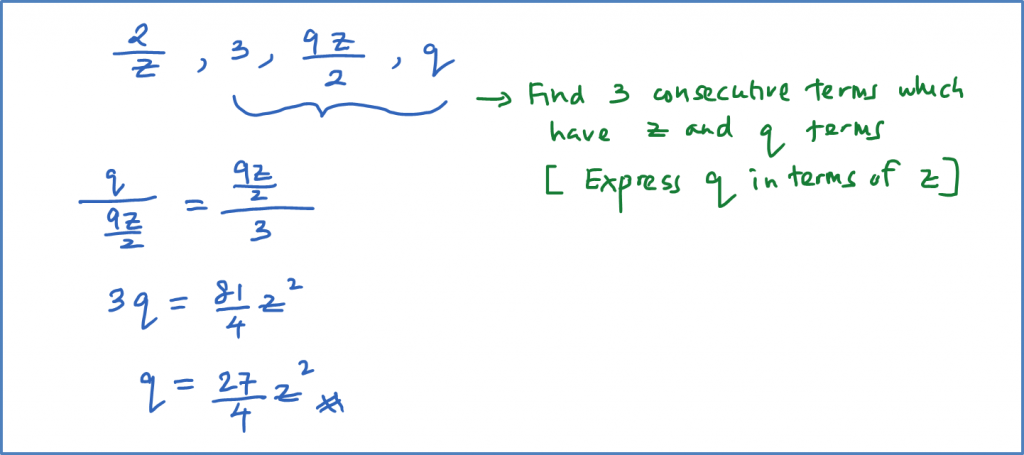
Question 7:
Given a geometric progression express q in terms of z.
Solution:
Given a geometric progression express q in terms of z.
Solution:

Question 8:
The second and the fourth term of a geometry progression are 10 and respectively. Find
(a) The first term and the common ratio where r > 0,
(b) The sum to infinity of the geometry progression.
Solution:

The second and the fourth term of a geometry progression are 10 and respectively. Find
(a) The first term and the common ratio where r > 0,
(b) The sum to infinity of the geometry progression.
Solution:

Question 9:
In a geometric progression, the first term is 18 and the common ratio is r.
Given that the sum to infinity of this progression is 21.6, find the value of r.
Solution:

In a geometric progression, the first term is 18 and the common ratio is r.
Given that the sum to infinity of this progression is 21.6, find the value of r.
Solution:

Question 10:
In a geometric progression, the first term is 27 and the fourth term is 1. Calculate
(a) the positive value of common ratio, r,
(b) the sum of the first n terms where n is sufficiently large till
Solution:
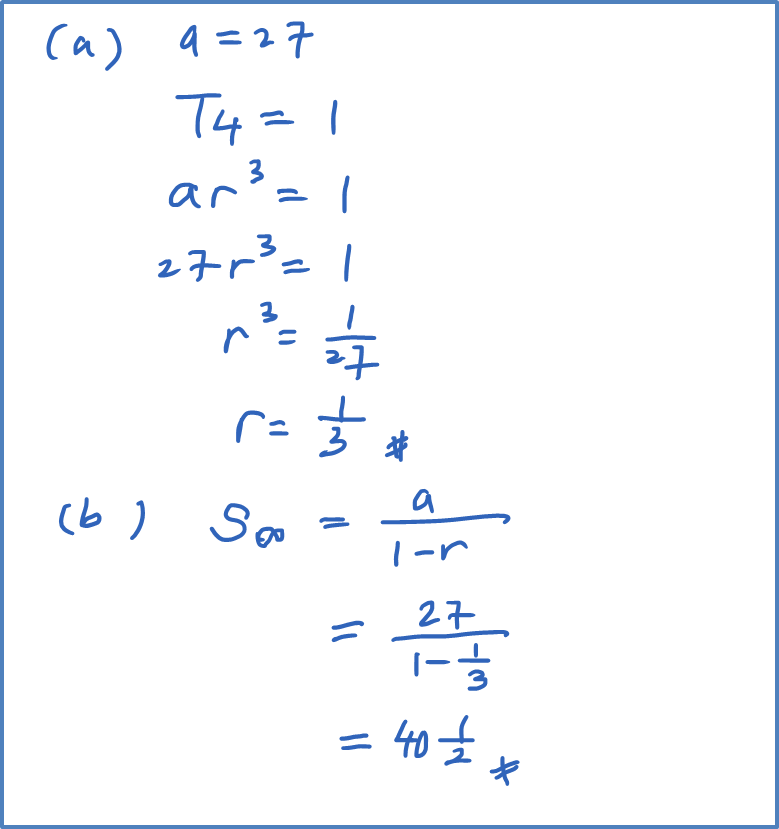
In a geometric progression, the first term is 27 and the fourth term is 1. Calculate
(a) the positive value of common ratio, r,
(b) the sum of the first n terms where n is sufficiently large till
Solution:
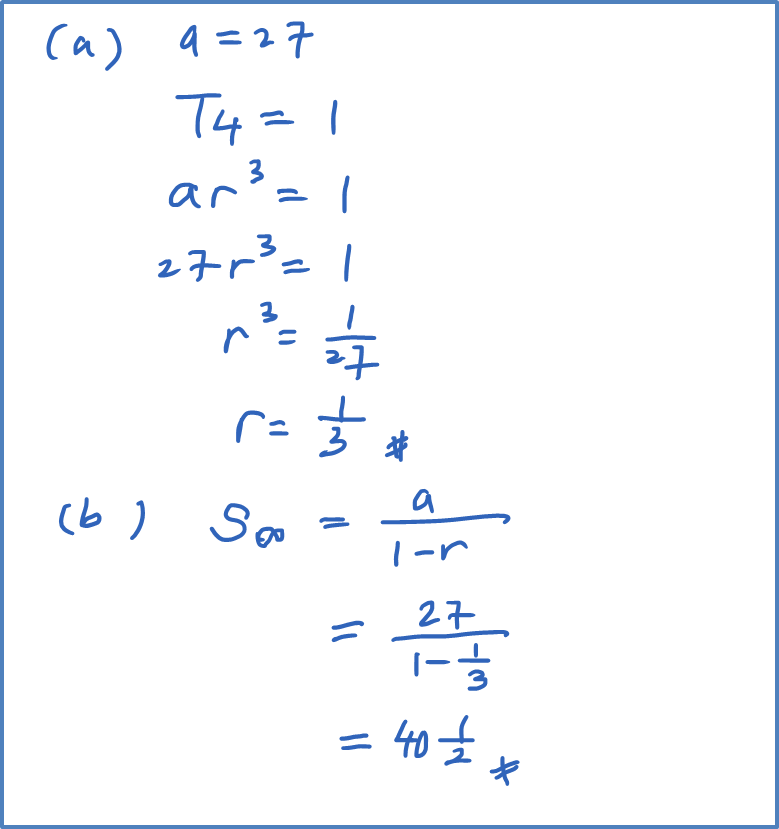
can u help me to open the next link
Dear Khadeja,
Please refresh the page if u couldn’t click the next page button.