Inverse Functions
1. Consider the function (f : x maps to – 2) with domain A = {1, 3, 4, 7}. Then the range of the function is B = {-1, 1, 2, 5}. The arrow diagram representing this function is shown as below.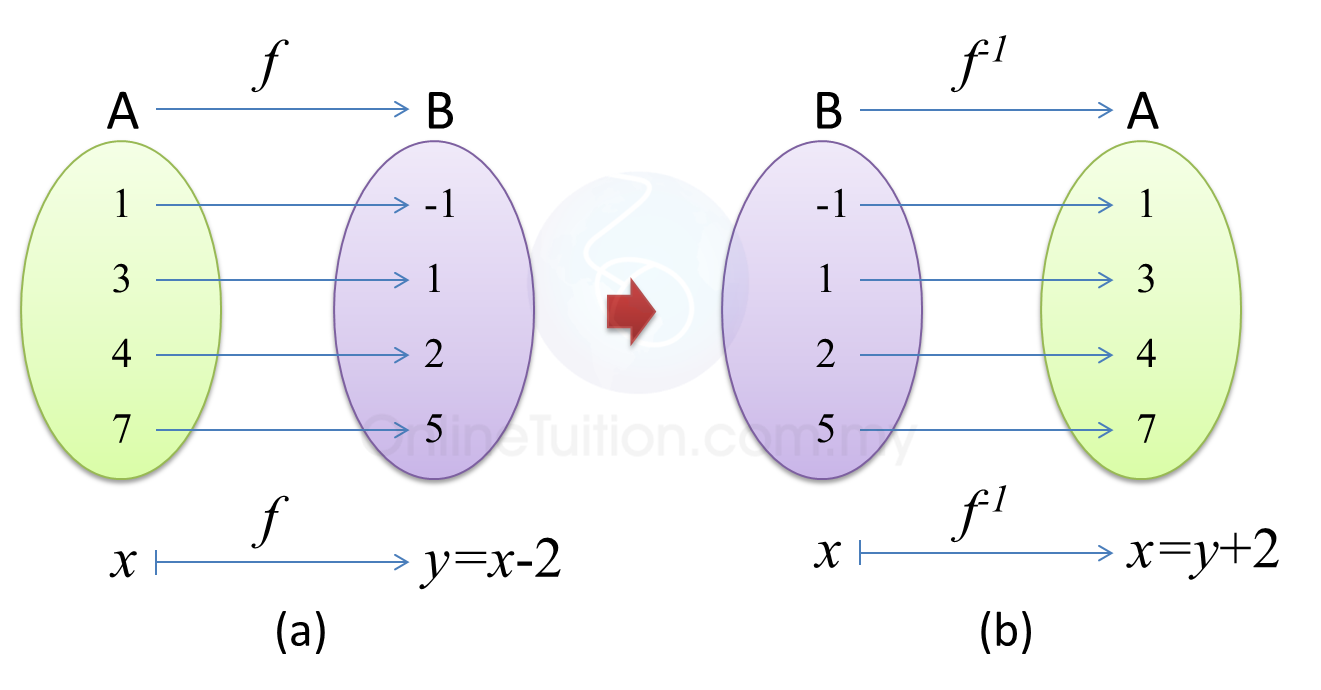
2. If the arrows of (a) are reversed, the arrow diagram in (b) is obtained. A new function having domain B and range A is formed from the function f. This new function is called the inverse function of f and is denoted by f-1 .
3. To Find the inverse function,
of
• Put the function equal to y.
• Rearrange to give x in term of y.
• Rewrite as replacing y by x.
Example: Given , find the inverse function.
• Put the function equal to y.
• Rearrange to give x in term of y.
• Rewrite as replacing y by x.
Example: Given , find the inverse function.
Example (Comparison Method)
Given that , x≠3k , where h and k are constants and , x≠0, find the value of h and of k.
Solution:
Given that , x≠3k , where h and k are constants and , x≠0, find the value of h and of k.
Solution:
