Question 1:
Solution:
(b)
(c)

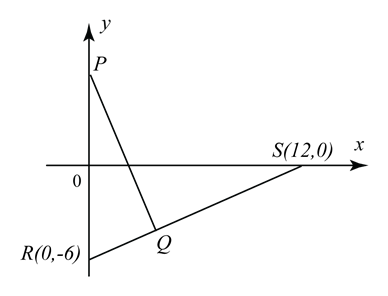
The diagram shows a straight line PQ which meets a straight line RS at the point Q. The point P lies on the y-axis.
(a) Write down the equation of RS in the intercept form.
(b) Given that 2RQ = QS, find the coordinates of Q.
(c) Given that PQ is perpendicular to RS, find the y-intercept of PQ.
(a)
Equation of RS
(b)
(c)
Point Q = (4, –4), m = –2
Using y = mx+ c
–4 = –2 (4) + c
c = 4
y–intercept of PQ = 4
Question 2:
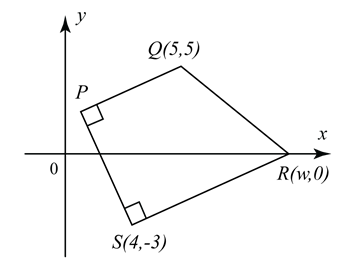
The diagram shows a trapezium PQRS. Given the equation of PQ is 2y – x – 5 = 0, find
Solution:
(a)
(b)
(c)
Hence, the equation of locus of the moving point M is

The diagram shows a trapezium PQRS. Given the equation of PQ is 2y – x – 5 = 0, find
(a) The value of w,
(b) the equation of PS and hence find the coordinates of P.
(c) The locus of M such that triangle QMS is always perpendicular at M.
Solution:
(a)
(b)
Point S = (4, –3), m = –2
y – y1 = m (x– x1)
y – (–3) = –2 (x – 4)
y + 3 = –2x + 8
y = –2x + 5
Equation of PS is y = –2x + 5
PS is y = –2x + 5—–(1)
PQ is 2y = x + 5—–(2)
Substitute (1) into (2)
2 (–2x + 5) = x + 5
–4x + 10 = x + 5
–5x = –5
x = 1
From (1), y = –2(1) + 5
y = 3
Coordinates of point P = (1, 3).
(c)
Hence, the equation of locus of the moving point M is
x2 + y2– 9x – 2y + 5 = 0.
helped me to warm up a little bit before exam. thx~~