Question 7:
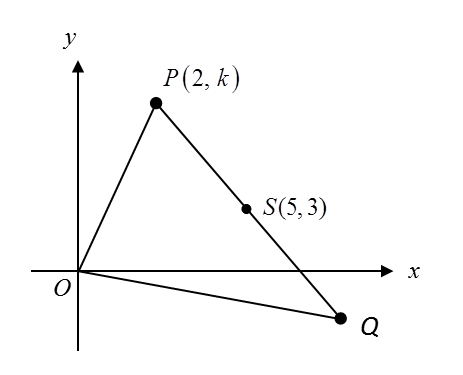
(a) A point Y moves such that its distance from point S is always 5 uints.
Solution:
(a)
(b)(i)
Solutions by scale drawing will not be accepted.
Diagram below shows a triangle OPQ. Point S lies on the line PQ.
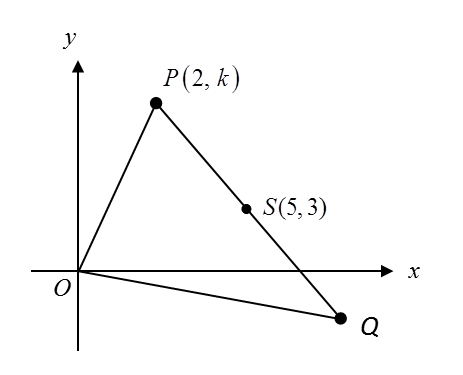
(a) A point Y moves such that its distance from point S is always 5 uints.
Find the equation of the locus of Y.
(b) It is given that point P and point Q lie on the locus of Y .
Calculate
(i) the value of k,
(ii) the coordinates of Q.
(c) Hence, find the area, in uint2, of triangle OPQ.
(c) Hence, find the area, in uint2, of triangle OPQ.
(a)
(b)(i)
Given P (2, k) lies on the locus of Y.
(2)2 + (k)2– 10(2) – 6(k) + 9 = 0
4 + k2– 20 – 6k + 9 = 0
k2 – 6k – 7 = 0
(k – 7) (k + 1) = 0
k = 7 or k = – 1
Based on the diagram, k = 7.
Based on the diagram, k = 7.
(b)(ii)
As P and Q lie on the locus of Y, S is the midpoint of PQ. P = (2, 7), S = (5, 3).
Let the coordinates of Q = (x, y),
(c)
Coordinates of point Q = (8, –1).
(c)
Question 8:
Diagram below shows a quadrilateral ABCD. Point C lies on the y-axis.
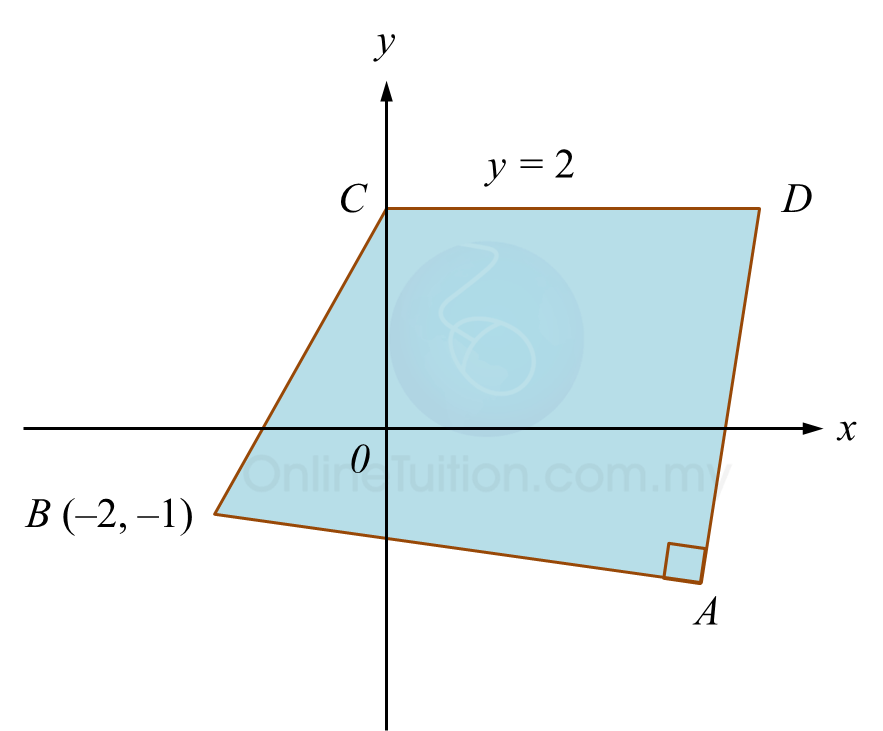
The equation of a straight line AD is 2y = 5x – 21
(a) Find
(i) the equation of the straight line AB,
(ii) the coordinates of A,
(b) A point P moves such that its distance from point D is always 5 units.
Find the equation of the locus of P.
Solution:
(a)(i)
(a)(ii)
(b)
Diagram below shows a quadrilateral ABCD. Point C lies on the y-axis.

The equation of a straight line AD is 2y = 5x – 21
(a) Find
(i) the equation of the straight line AB,
(ii) the coordinates of A,
(b) A point P moves such that its distance from point D is always 5 units.
Find the equation of the locus of P.
Solution:
(a)(i)
(a)(ii)
(b)
for 7b (ii), how do i know that S is the midpoint of PQ? its not given in the question thanks
Hi Tye,
It is given in the question that point P and point Q lie on the locus of Y.
PSQ is a straight line and SP = SQ = 5 units, therefore S is the midpoint of PQ.