Change of Base of Logarithms
Example:
Find the value of the following:
a.
b.
Answer:
Example 1
Find the value of the following.
(a)
(b)
(c)
(d)
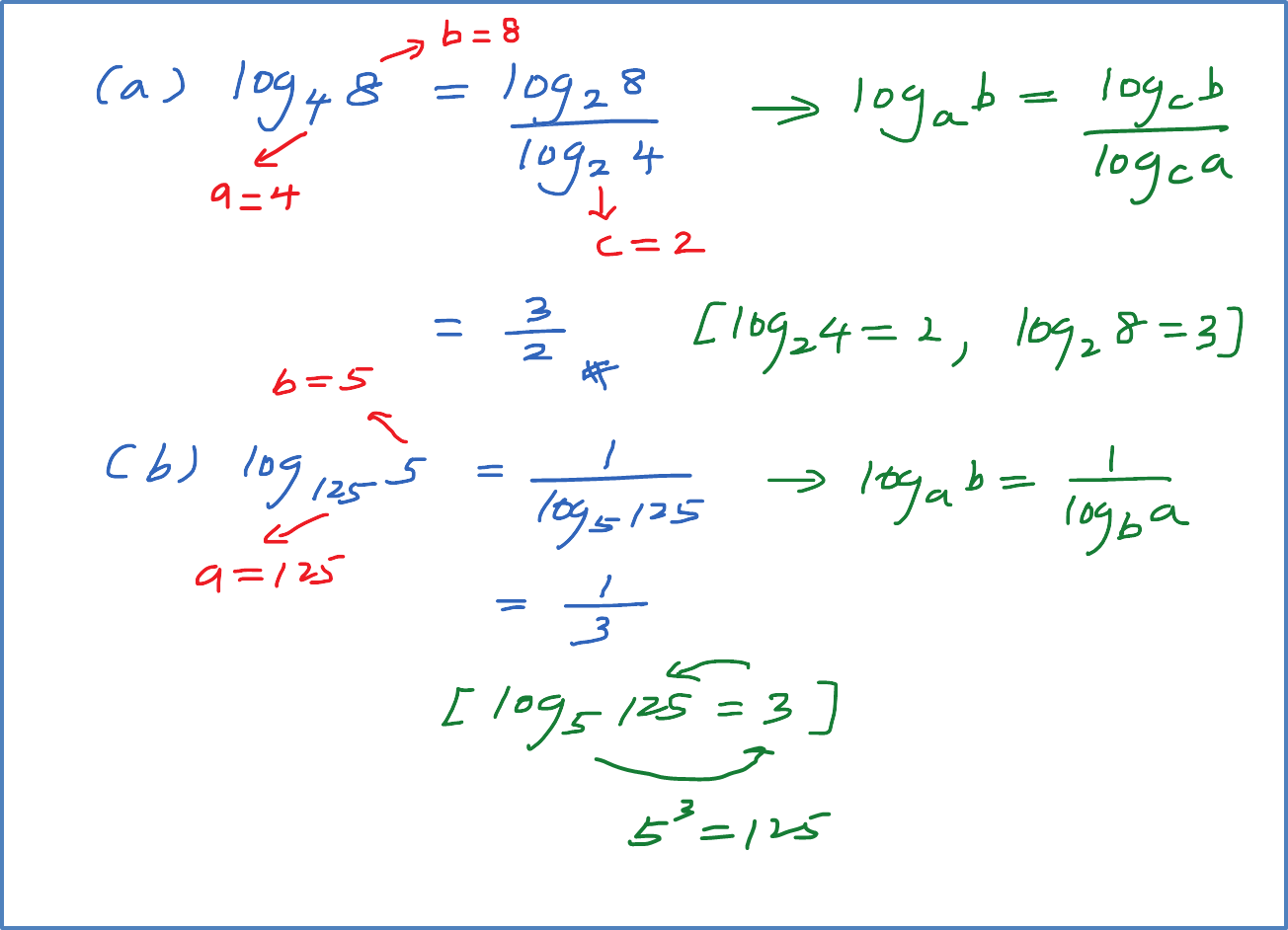
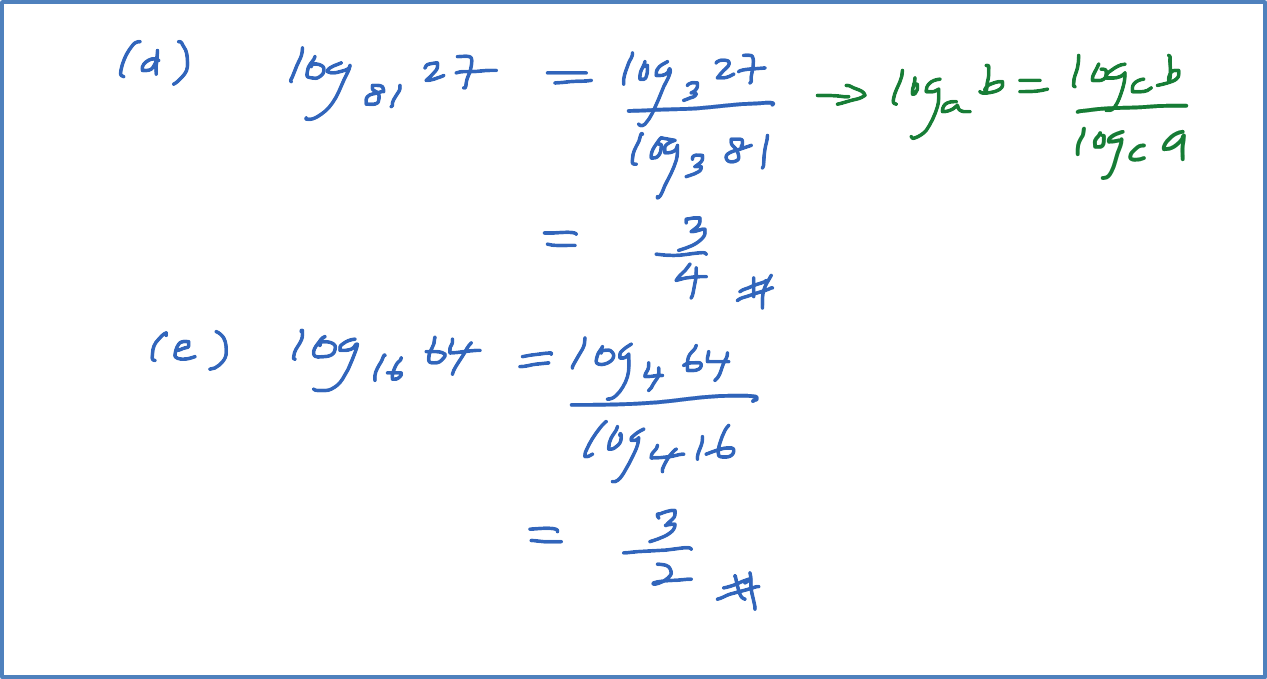
Find the value of the following.
(a)
(b)
(c)
(d)
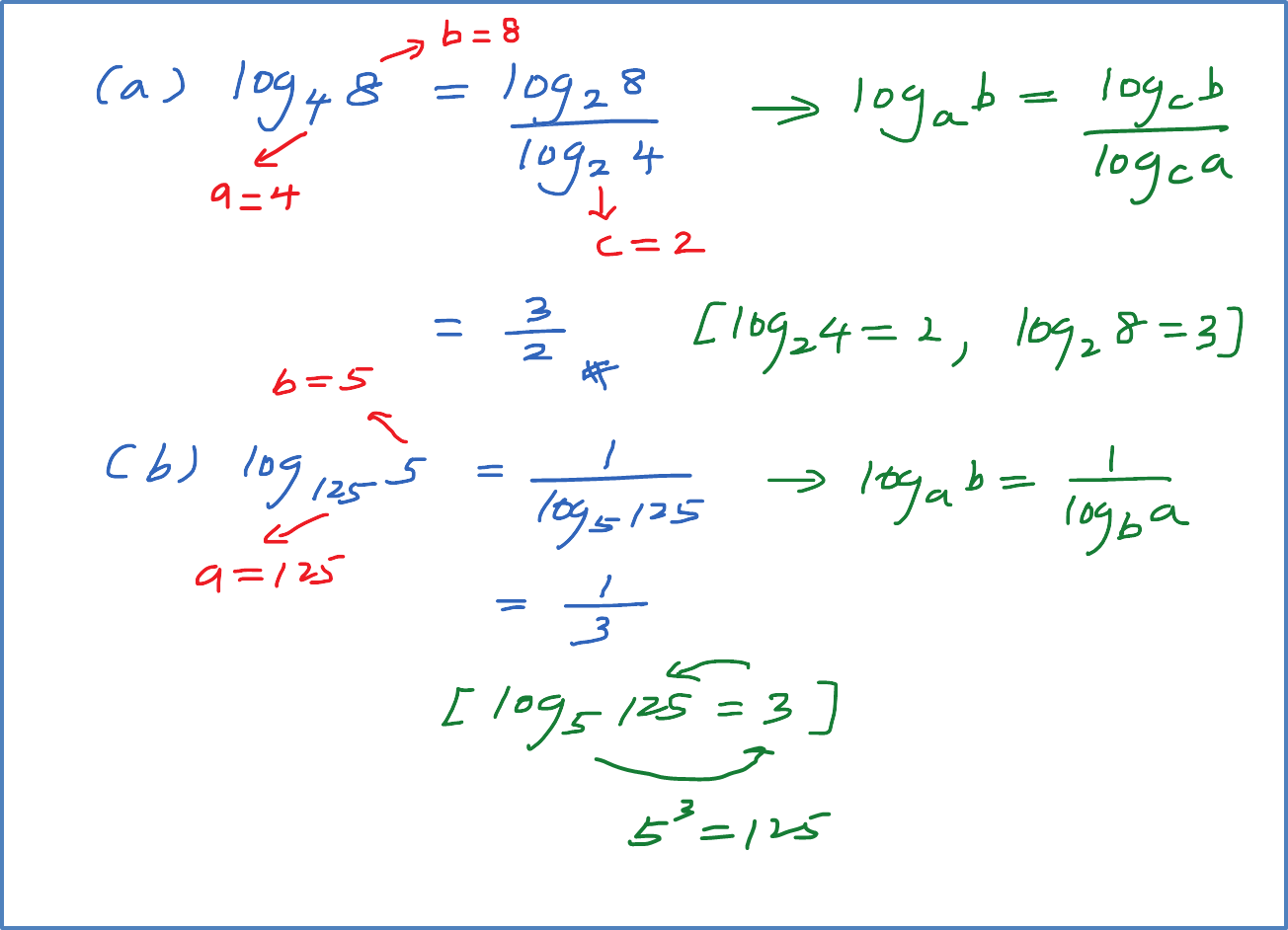
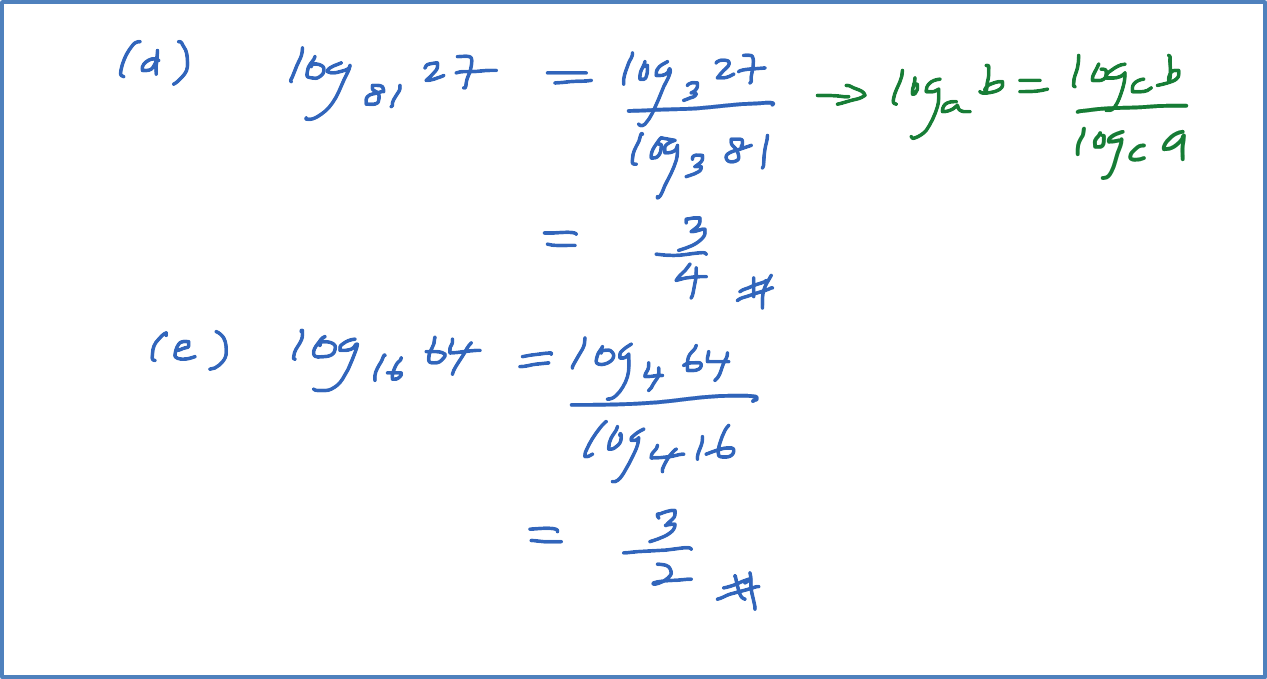
Example 2
Given that and , express the following in term of h and or k.
(a)
(b)
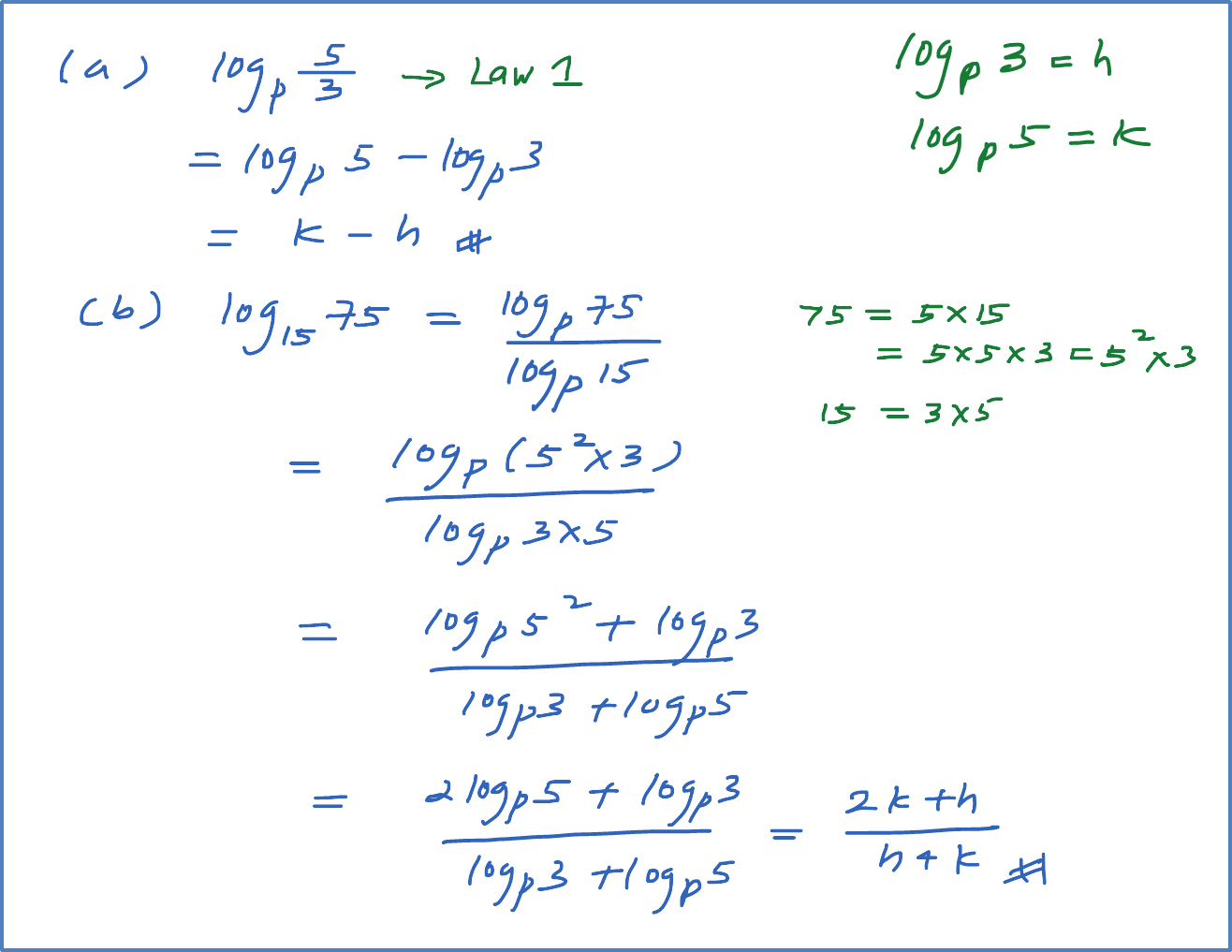
Given that and , express the following in term of h and or k.
(a)
(b)
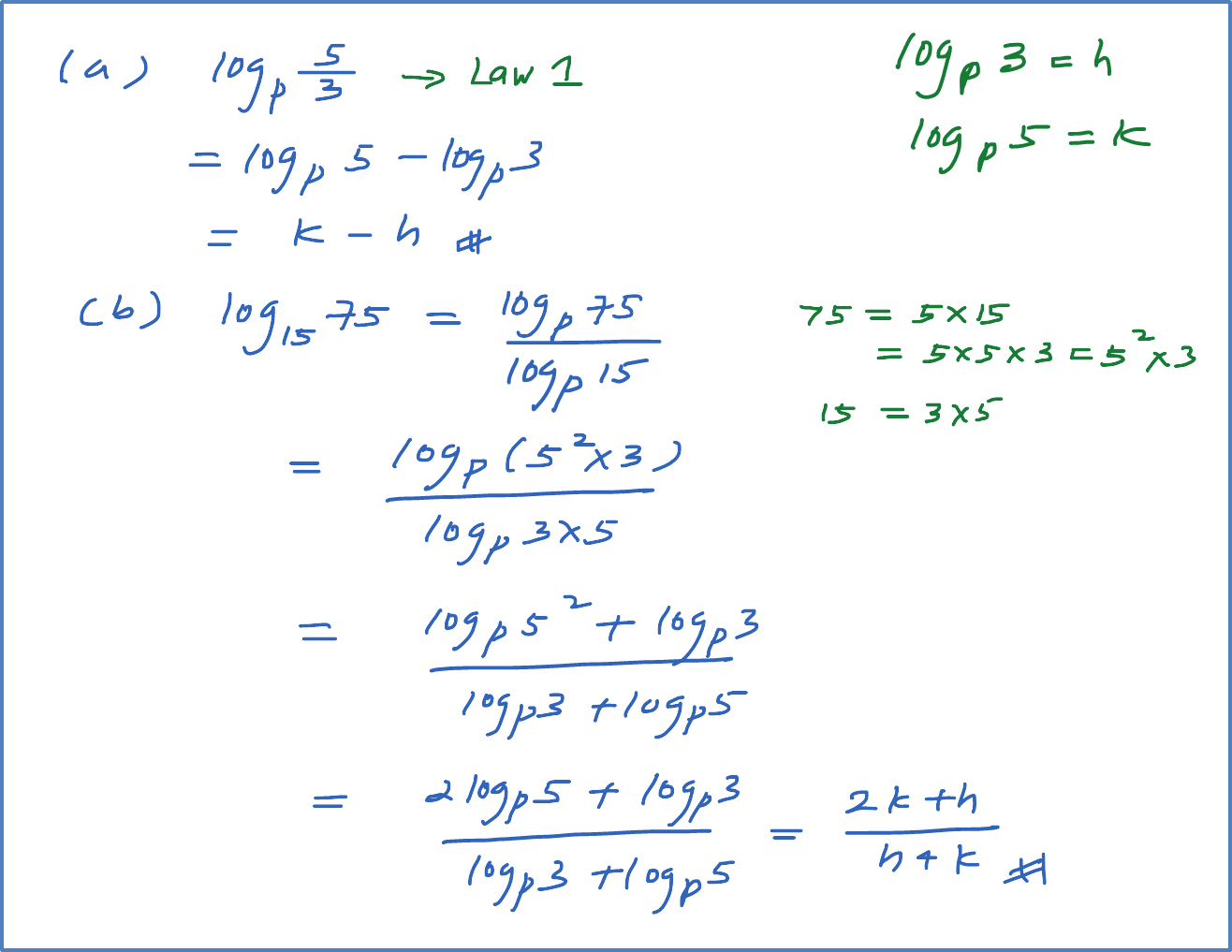
a. log 100 should be log 10 to the power of 2, equal 2