2.3.2 Solving Quadratic Equations – Completing the Square
(A) The Perfect Square
(A) The Perfect Square
1. The expression x2 + 2x + 1 can be written in the form (x + 1)2, it is called a “perfect square”.
2. If the algebraic expression on the left hand side of the quadratic equation is a perfect, the roots can be easily obtained by finding the square roots.
Example:
Solve each of the following quadratic equation
Solve each of the following quadratic equation
(a) (x + 1)2 = 25
(b) x2 − 8x + 16 = 49
Solution:
(a)
(x + 1)2 = 25
(x + 1)2 = ±√25
x = −1 ± 5
x = 4 or x = −6
(b)
x2 − 8x + 16 = 49
(x − 4)2 = 49
(x − 4) = ±√49
x = 4 ± 7
x = 11 or x = −3
(B) Solving Quadratic Equation by Completing the Square
1. To solve quadratic equation, we make the left hand side of the equation a perfect square.
2. To make any quadratic expression x2 + px into a perfect square, we add the term (p/2)2 to the expression and this will make
3. The following shows the steps to solve the equation by using completing the square method for quadratic equation ax2+ bx = – c.
(a) Rewrite the equation in the form ax2 + bx = – c.
(b) If the coefficient a ≠ 1, reduce it to 1 (by dividing).
(c) Add or to both sides of the equation.
(d) Write the expression on the left hand side as a perfect square.
(e) Solve the equation.
Example:
Solve the following quadratic equations by completing the square.
(a) x2 – 6x – 3 = 0
(a) x2 – 6x – 3 = 0
(b) 2x2 – 5x – 7 = 0
(c) x2 + 1 = 10x/3
Solution:
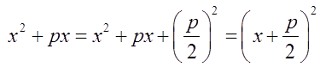




a)x=4 or -6 right?
Dear Aini,
Thanks for pointing out our mistake.
Correction was done accordingly.